Question

What is the area bounded by the curves? : `4x + y^2 = 32` and `x=y`

Answer 1

We have:

`4x + y^2 = 32`
`x=y`

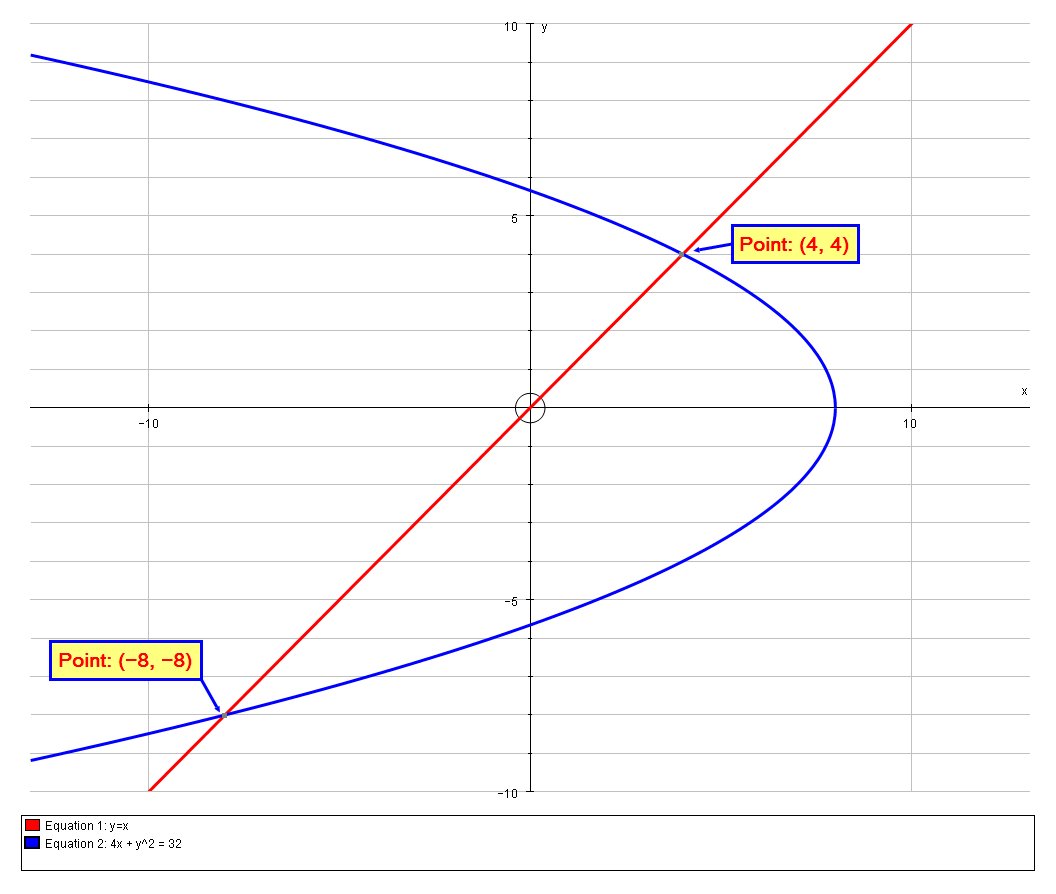
The graphs are as follows:

To find the coordinates of intersection:

`4x + x^2 = 32`
`:. (x-4)(x+8) = 0`
`=> x=4, -8`

So the intersection coordinates are:

`(-8,-8)` and `(4,4)`

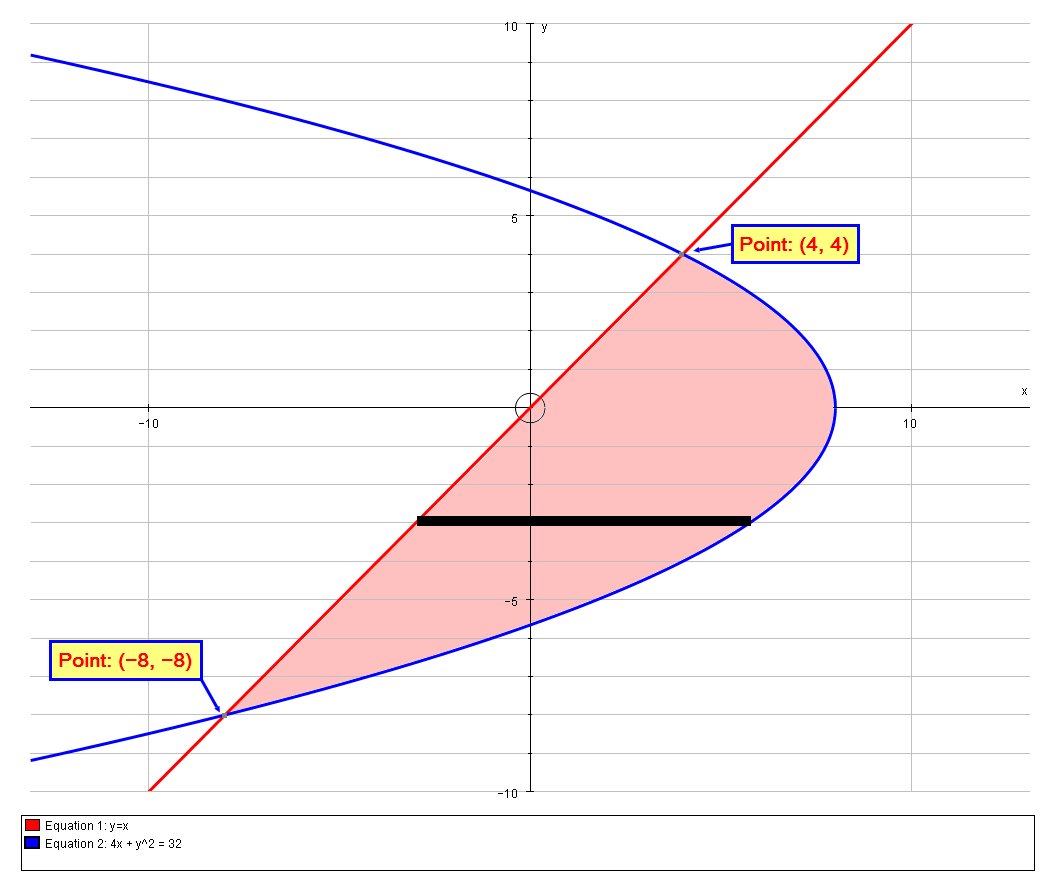
We can calculate the bounded area (shaded) by integrating either wrt `x` or wrt `y`, the latter being easier.

Method 1: Integrating wrt `y`

if we integrate with infinestimall thin horiozontal striops then we find the strips are bounded by `y=x` on the left and by `4x + y^2 = 32` on the right, and we integrate from the lower point of intersection`(-8,-8)` to the upper point of intersection `(4,4)`.

Thus, the area is given by:

`A = int_alpha^beta \ f(y) \ dy`
`\ \ \ = int_(y=-8)^(y=4) \ ( (32-y^2)/4 ) -(y) \ dy`
`\ \ \ = int_(-8)^(4) \ 8 - y^2/4 -y \ dy`
`\ \ \ = [ 8y - y^3/12 -y^2/2 ]_(-8)^(4)`
`\ \ \ = (32-16/3-8) - (-64+128/3-32)`
`\ \ \ = 56/3 - (-160/3)`
`\ \ \ = 72`

Method 2: Integrating wrt `x`

if we integrate with infinestimall thin vertical striops then we find the strips are bounded by `4x + y^2 = 32` at the bottom and `y=x` at the top but only when `x` is between the lower point of intersection`(-8,-8)` to the upper point of intersection `(4,4)`

We also need to include a portion that is bounded by `4x + y^2 = 32` at the top and bottom between the upper point of intersection and the vertex (at `x=8`).

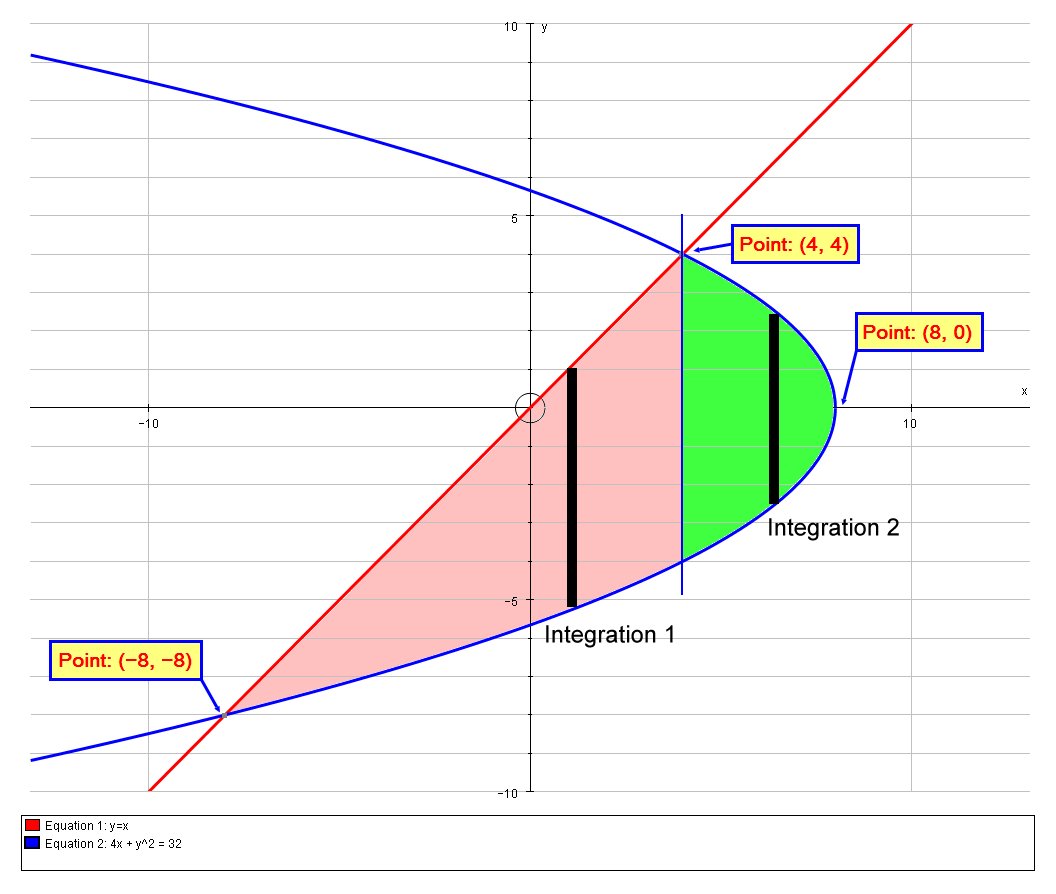
Thus, the area is split into two seperate integrals:

`A = A_1 + A_2`

Where:

`A_1 = int_(x=-8)^(x=4) (x)-(-sqrt(32-4x)) \ dx`
`A_2 =int_(x=4)^(x=8) \ (sqrt(32-4x) - (-sqrt(32-4x) ) \ dx`

First we calculate `A_1`:

`A_1 = int_(-8)^(4) x+sqrt(32-4x) \ dx`
`\ \ \ \ = [x^2/2 -(4(8-x)^(3/2))/3 ]_(-8)^(4)`
`\ \ \ \ = (8-32/3) - (32 - 256/3)`
`\ \ \ \ = (-8/3) - (-160/3)`
`\ \ \ \ = 152/3`

Then, `A_2`

`A_2 =int_(4)^(8) \ 2sqrt(32-4x) \ dx`
`\ \ \ \ = 2 int_(4)^(8) \ sqrt(32-4x) \ dx`
`\ \ \ \ = 2 [-(4(8-x)^(3/2))/3 ]_(4)^(8)`
`\ \ \ \ = 2 { (0) - (-32/3) }`
`\ \ \ \ = 64/3`

So, the total area is:

`A = A_1 + A_2`
`\ \ \ = 152/3 + 64/3`
`\ \ \ = 72`