To solve the first inequality, divide each side of the inequality by #color(red)(2)# to solve for #x# while keeping the inequality balanced:
#(2x)/color(red)(2) < 10/color(red)(2)#
#(color(red)(cancel(color(black)(2)))x)/cancel(color(red)(2)) < 5#
#x < 5#
To solve the second inequality, divide each side of the inequality by #color(blue)(-5)# to solve for #x# while keeping the inequality balanced. However, because we are multiplying or dividing an inequality by a negative term we must reverse the inequality operator:
#(-5x)/color(blue)(-5) color(red)(>) 5/color(blue)(-5)#
#(color(blue)(cancel(color(black)(-5)))x)/cancel(color(blue)(-5)) color(red)(>) -1#
#x > -1#
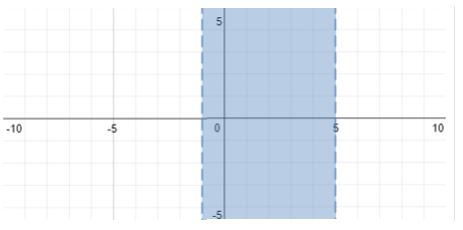
The solution is: #x > -1# and #x < 5#
Or, in interval notation: #(-1, 5)#
To graph this we will draw two vertical lines at #-1# and #5# on the horizontal axis.
The lines will be dashed lines because the inequality operators do not contain an "or equal to" clause.
We will shade between the interval of the lines: