How do you graph #f(x)=4(3/4)^(x+1)-5# and state the domain and range?

Question

992 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-11-08T19:36:50

See below.

The y axis intercept occurs where #x=0#, so:

#4(3/4)^(0+1)-5=-2 # coordinate #( 0 , -2)#

There are no restrictions on #x# so:

Domain is #{ x in RR }#

#lim_(x->oo)4(3/4)^(x+1)-5=-5# ( y = -5 is a horizontal asymptote )

For #x< -1#

#4(3/4)^(x+1)-5# becomes:

#4/((3/4)^(x+1))-5#

as #x->oo# ,# (3/4)^(x+1)->0#

So:

#lim_(x->-oo)4(3/4)^(x+1)-5=oo#

Range is:

#{y in RR: -5 < y < oo}#

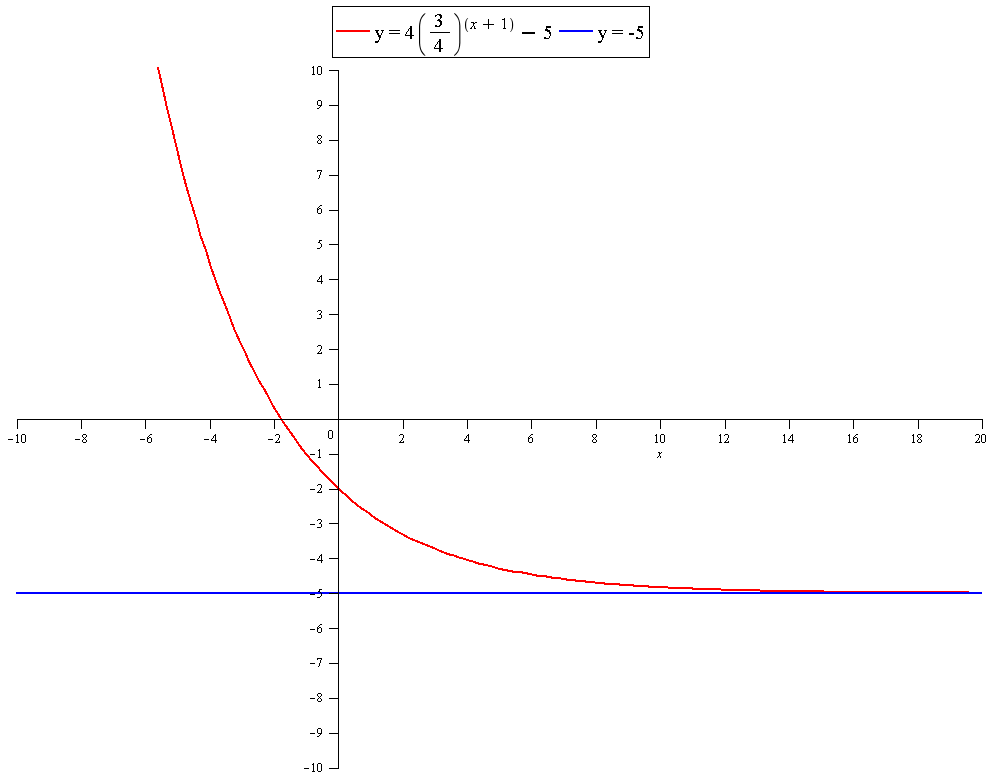
Graph:

enter image source here