How do you graph #f(x)=-(2/3)^x+3# and state the domain and range?
1 Answer
Nov 11, 2017
See below.
Explanation:
First find any
as
as
The line
Graph:
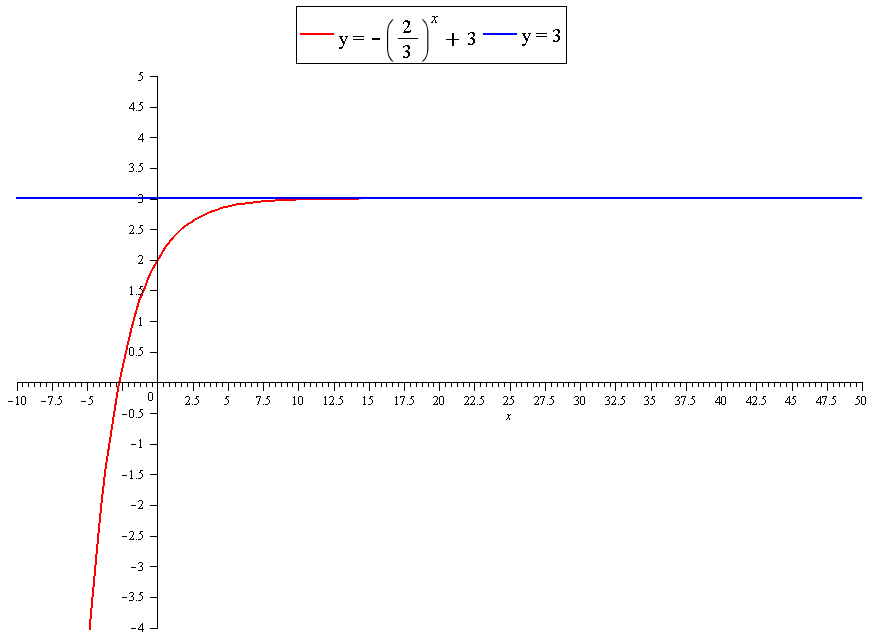
See below.
First find any
as
as
The line
Graph:
