Question

How do you graph the parabola `y=x^2-3x+8` using vertex, intercepts and additional points?

Answer 1

For `y=ax^2+bx+c` the `x` for vertex is

`x_v=-b/(2a)=3/2`

so

`y_v=x^2−3x+8 = (3/2)^2-3*3/2+8= 23/4`

So the vertex is `( 3/2,23/4)`.

Since `a>0`, so it is looking up.
The `y`-intercept is `Y=0^2-3*0+8=8` so `(0,8)`

Explanation:

After finding the `y`-intercept, we should practically find the `x`-intercept, but as you see, the graph is looking upward since `a` is bigger than `0` and the vertex is higher than `0`.

So there will be no `x`-intercept, meaning that the graph will not intersect the `x`-axis. You can just plug in any number and then use the symmetrical characteristic of the hyperbola and draw the whole thing.

Answer 2

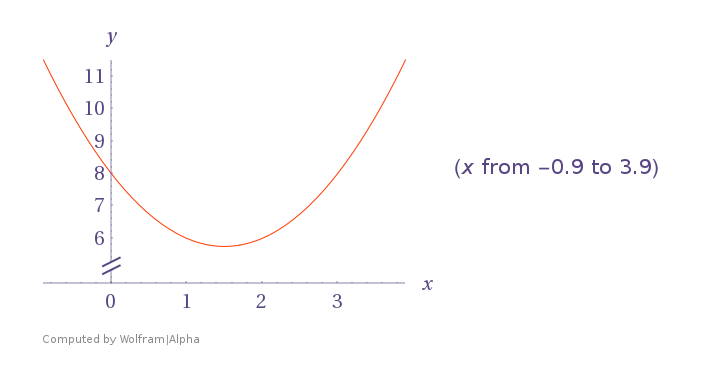
Vertex: `(\frac{3}{2},\frac{23}[4})`

`y`-intercept: `(0,8)`

Other point: `(3,8)`

Explanation:

We can find the `x`-coordinate of the vertex by using the formula `-\frac{b}{2a}`, where `a` and `b` come from the standard form of `ax^2+bx+c`.

In this equation,

• `a=1`
• `b=-3`
• `c=8`

Plugging in yield:

`-\frac{-3}{2(1)}\quad\implies\quad \frac{3}{2}`

To find the `y`-coordinate of the vertex, plug the `x`-coordinate into the equation in standard form:

`x^2-3x+8`

`\implies (\frac{3}{2})^2-3(\frac{3}{2})+8`

`\implies \frac{9}{4}-\frac{9}{2}+8`

`\implies -\frac{9}{4}+8`

`\implies \frac{23}{4}`

`\therefore` the vertex is `(\frac{3}{2},\frac{23}{4})`.

---

The `y`-intercept is simply `(0,c)`, which is `(0,8)` in this case.

---

For a third point, we can find the axis of symmetry of the parabola, and reflect the `y`-intercept across that line.

The axis of symmetry is the vertex’s `x`-coordinate, which is `1.5`.

`\therefore` the third point will have an `x`-coordinate of `1.5\cdot 2`, which is `3`. The `y`-coordinate is the same as the `y-`-intercept, which is `8`.

`\therefore` a third point is `(3,8)`.

That’s all we need to graph a parabola.

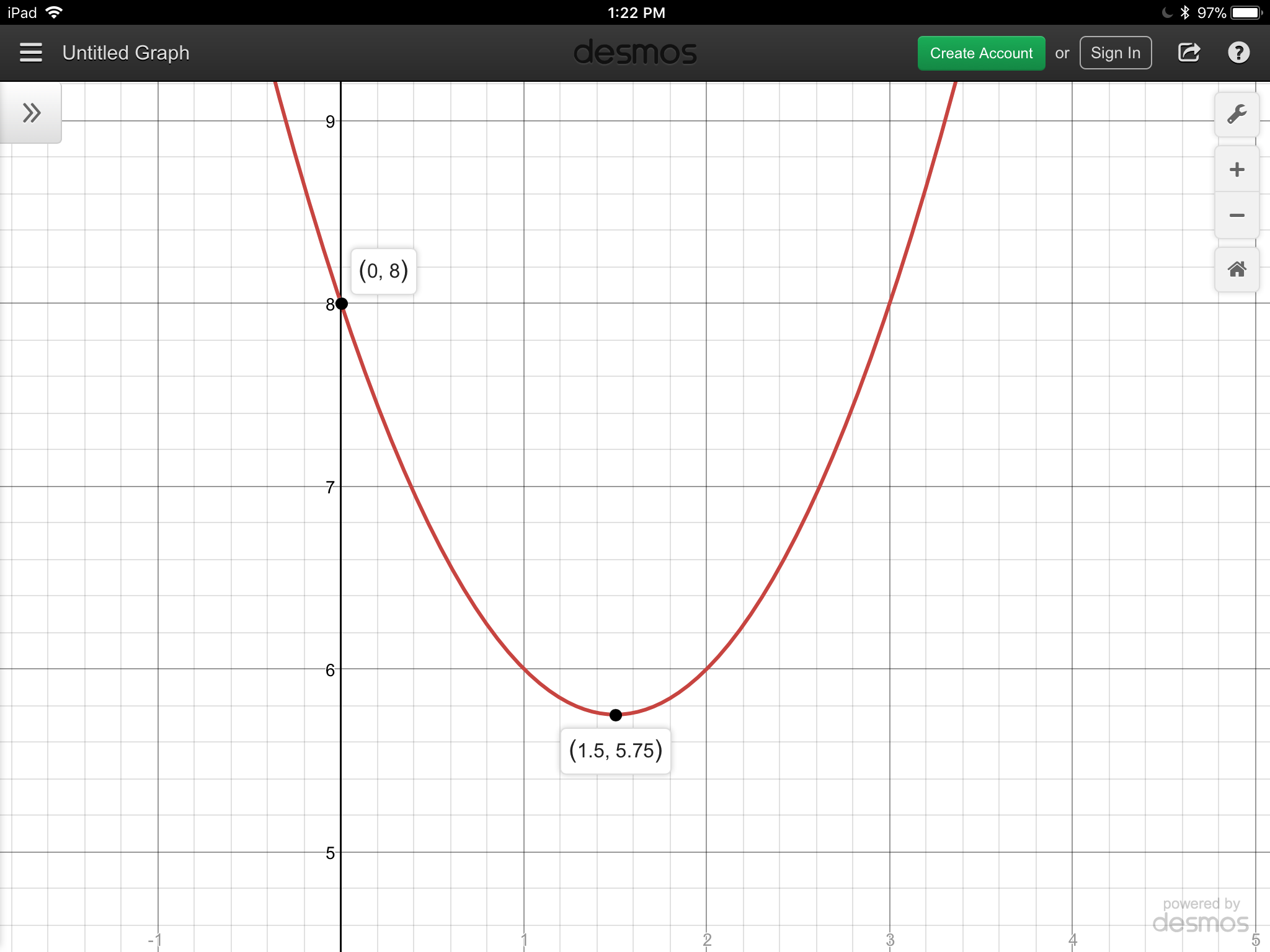Desmos