A parallelogram has sides with lengths of #7 # and #15 #. If the parallelogram's area is #8 #, what is the length of its longest diagonal?
1 Answer
Dec 5, 2017
Explanation:
Let the parallelogram
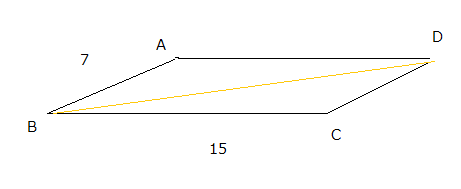
(I'm not good at drawing figures.The acutual parallelogram would be far flatter.)
Then,
If the parallelogram's area is
Let
As
Then, calculate

