Question #ff8f4
1 Answer
Here's my take on this.
Explanation:
This is a bit difficult to decipher without more information, but my guess would be that you're looking at the alpha decay of plutonium-244,
For starters, it;'s worth mentioning that the PeriodicTable tells you the average atomic mass of plutonium, i.e.
If you round the atomic mass of plutonium to the nearest whole number, you will get the mass number of the most abundant isotope of plutonium, which in this case, is plutonium-244.
244.064≈244
Since plutonium has an atomic number equal to
244−94=150
neutrons inside its nucleus. This is the case because the mass number of a nuclide is calculating by adding the number of protons, which is given by the atomic number, and the number of neutrons.
Now, when plutonium-244 undergoes alpha decay, it emits an alpha particle, which is essentially the nucleus of a helium-4 isotope.
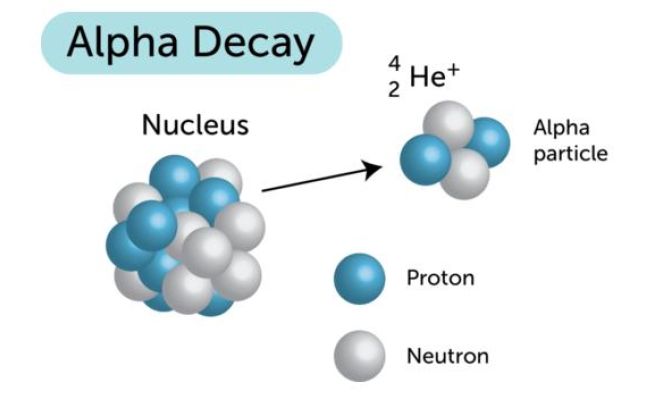http://www.ck12.org/book/CK-12-Physical-Science-Concepts-For-Middle-School/section/3.60/
This means that the nuclear equation that describes the alpha decay of plutonium-244 looks like this
244194Pu→240192U+42α
This is the case because an alpha particle contains
In order for charge and mass to be conserved, you need to have
244=240+4→ conservation of mass94=92+2 → conservation of charge
This is why the resulting nuclide, uranium-240, has a mass number equal to
ALTERNATIVE INTERPRETATION
Now that I think about it, it's possible that you're referring to plutonium-240, an isotope of plutonium.
This isotope has a mass number equal to
240−94=146
neutrons inside the nucleus, as opposed to
As you know, isotopes are atoms that have the same number of protons, i.e. the same atomic number, but different numbers of neutrons, i.e. different mass numbers.
In this case, both plutonium-240 and plutonium-244 have
