Question

How do you find the amplitude, period, and shift for `y = -5sin(x/2)`?

Answer 1

Amplitude `= |A| = |-5| = 5`

Period `" "=(2Pi)/(1/2) = 4Pi`

Shift `" "= C/B = 0/(1/2) = 0`

The Vertical Shift (D) = 0

Explanation:

Investigate the graph given below:

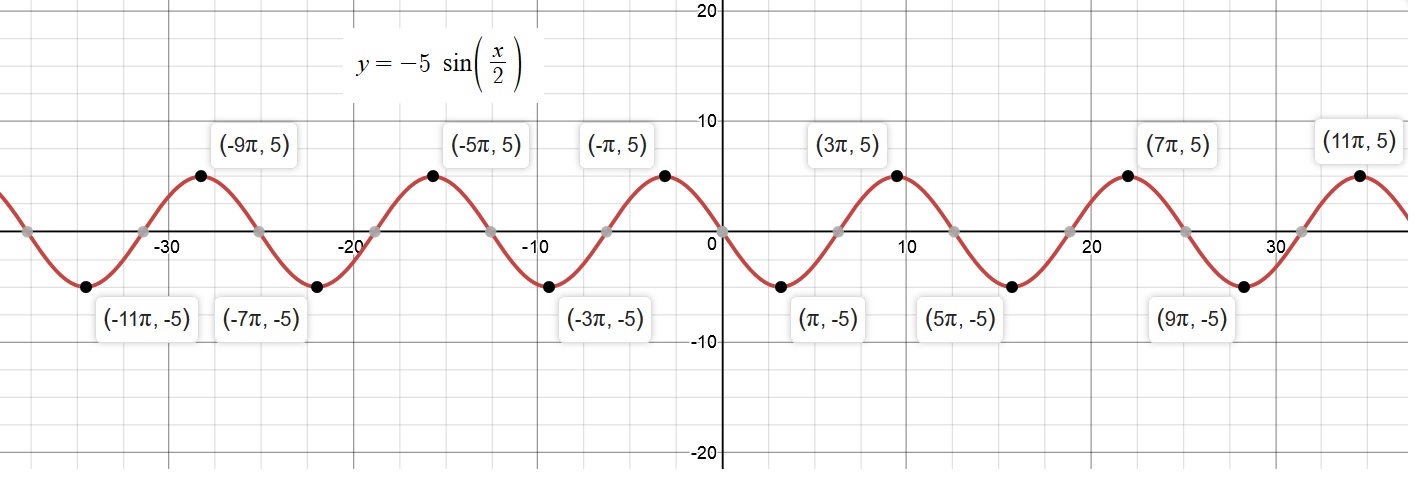
The General Form of the equation of the Cos function:

`color(green)(y = A*Sin(Bx + C) + D)`, where

A represents the Vertical Stretch Factor and its absolute value is the Amplitude.

B is used to find the Period (P):`" "P = (2Pi)/B`

C, if given, indicates that we have a place shift BUT it is NOT equal to `C`

The Place Shift is actually equal to `x` under certain special circumstances or conditions.

D represents Vertical Shift.

We observe that

Amplitude `= |A| = |-5| = 5`

Period `" "=(2Pi)/(1/2) = 4Pi`

Shift `" "= C/B = 0/(1/2) = 0`

The Vertical Shift (D) = 0

Hope this helps.

Answer 2

`5,4pi,0,0`

Explanation:

`"the standard form of the sine function is "`

`color(red)(bar(ul(|color(white)(2/2)color(black)(y=asin(bx+c)+d)color(white)(2/2)|)))`

`"where amplitude "=|a|," period "=(2pi)/b`

`"phase shift "=-c/b" and vertical shift "=d`

`"here "a=-5,b=1/2,c=d=0`

`"amplitude "=|-5|=5," period "=(2pi)/(1/2)=4pi`

`"there is no phase / vertical shift"`