A solid consists of a cone on top of a cylinder with a radius equal to that of the cone. The height of the cone is #33 # and the height of the cylinder is #13 #. If the volume of the solid is #2750 pi#, what is the area of the base of the cylinder?

Question

5138 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-01-10T04:54:18

Base area of the cylinder

#A_(cyl) = pi r^2 = pi (7.73)^2 = color (blue)(24.29)#

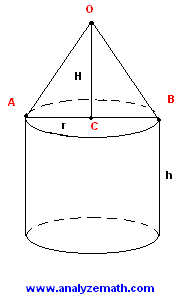
enter image source here

Volume of the solid #V_s = 2750pi#

Height of cone #h = 33#

Height of cylinder #H = 13#

V_(cone) = (1/3)pi r^2h#

#V_(cyl) = pi r^2 H#

V_s #= volume of cylinder + volume of cone

#V_s = pi r^2 H + (1/3) pi r^2 h#

#2750 cancel(pi) = cancel(pi) r^2 (H + h)#

#r^2 = 2750 / (13 + 33) = 59.78#

#r ~~ 7.73#

Base area of the cylinder

#A_(cyl) = pi r^2 = pi (7.73)^2 = color(blue)(24.29)#