An object with a mass of 7 kg is on a surface with a kinetic friction coefficient of 8 . How much force is necessary to accelerate the object horizontally at 32 m/s^2?
2 Answers
Jan 14, 2018
Explanation:
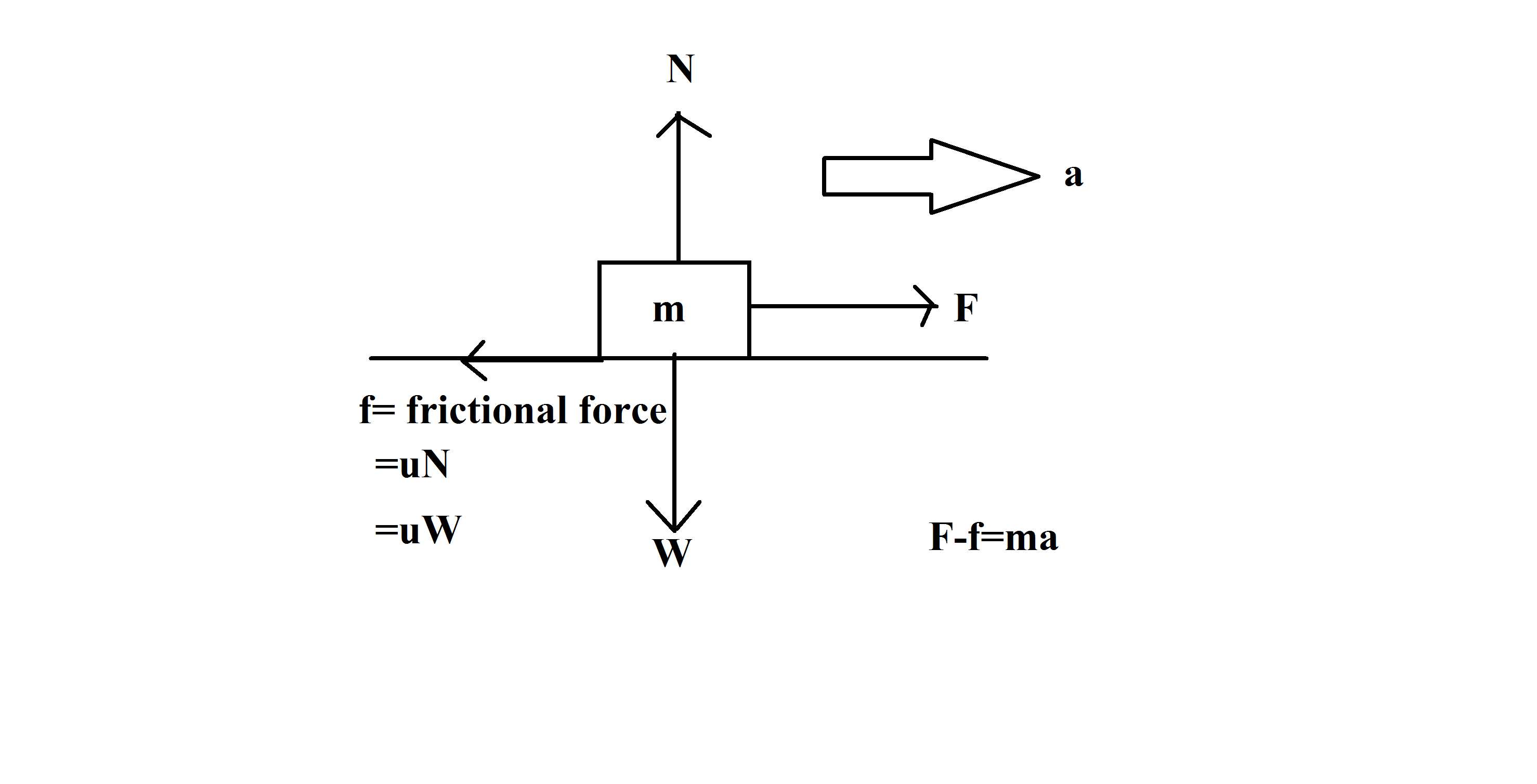 As,the object is going on a horizontal surface,frictional force acting on it will be
As,the object is going on a horizontal surface,frictional force acting on it will be
So,le't's assume we will be requiring a force of F to cause an acceleration of 32 SI units on it.
so,we can write,
so,
Jan 14, 2018
The force is
Explanation:
The mass of the object is
The acceleration is
The coefficient of kinetic friction is
The normal force is
The frictional force is
The force necessary to accelerate the object is
The acceleration due to gravity is
According to Newton's Second Law


