Question

How do you find the max or minimum of `f(x)=4x-x^2+1`?

Answer 1

`"maximum at "(2,5)`

Explanation:

`f(x)=-x^2+4x+1larrcolor(blue)"in standard form"`

`"with "a=-1,b=4" and "c=1`

`• " if "a>0" then f(x) has a minimum "uuu`

`• " if "a<0" then f(x) has a maximum "nnn`

`"here "a=-1<0rArr"f(x) has a maximum"`

`"the max/min is at the vertex of the parabola"`

`"to find the vertex use "color(blue)"completing the square"`

`rArrf(x)=-(x^2-4x-1)`

`color(white)(xxxxxx)=-(x^2+(-2)x+4-4-1)`

`color(white)(xxxxxx)=-(x-2)^2+5`

`rArr"vertex at "(2,5)`

`rArr"maximum at "(2,5)`
graph{(y+x^2-4x-1)((x-2)^2+(y-5)^2-0.04)=0 [-10, 10, -5, 5]}

Answer 2

Maximum is at : `color(blue)[(2,5)`

Explanation:

Given:

`color(red)(y = f(x) = 4x - x^2 +1)`

`rArr f(x) = - x^2 + 4x +1`

`Let " " f(x) = - x^2 + 4x +1 = 0` ...(1)

The Standard Form of a Quadratic Equation is:

`f(x) = ax^2 + bx + c = 0`

If `a > 0` then

the y coordinate value of the vertex represents a Minimum

If `a < 0` then

the y coordinate value of the vertex represents a Maximum

Hence, we have a Maximum for our problem.

Also, remember that

Vertex:

`[ ((-b)/(2a)), f((-b)/(2a))]`

From .... (1) we observe that

`color(blue)(a = -1; b = 4 and c = 1)`

x coordinate of the vertex:

`(-b)/(2a) = (-4)/(2(-1)) = ((-4)/-2) = 2`

Substitute the value of the x coordinate in (1) to get the y coordinate value

`y = - x^2 + 4x +1`

`rArr -(2)^2 + 4(2) + 1`

`rArr -4 + 8 + 1`

`rArr 5`

`:.` Vertex: `color(blue)[(2,5)`

Hence,

Maximum is at : `color(blue)[(2,5)`

Analyze the graph below to understand the behavior of the quadratic:

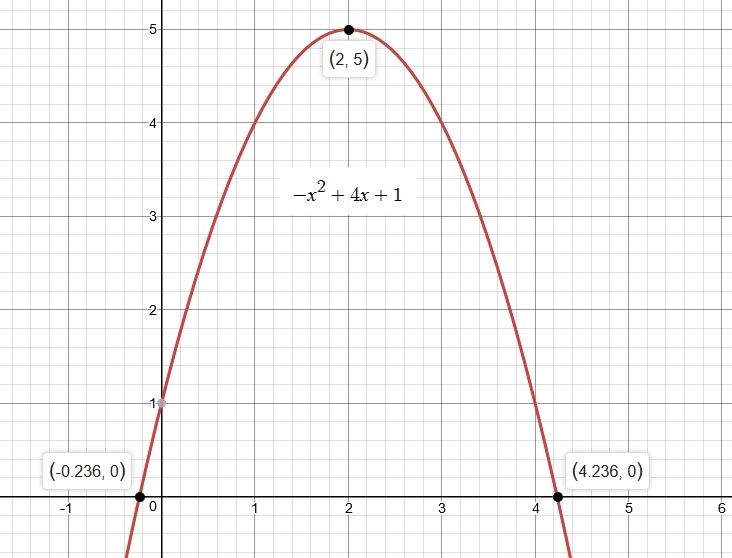
Hope you find this solution useful.