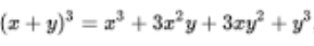How do you find the 2nd term in the expansion of #(y-x)^4#?
1 Answer
Use binomial theorem to determine the coefficients of the second term and the exponents of y and x in that term.
Explanation:
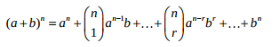
This equation above allows you to calculate any term in a binomial relationship as long as you know "n", which in this case is 4.
The first term according to this formula would be a^n or in your case, y^4.
In order to find the second term, you need to use the next term that is in the equation:
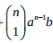
But in order to use this equation above, we need to understand what the brackets mean and how to calculate them.
The brackets are what allow you to calculate the coefficient of the term. The coefficient can be calculated using this equation....
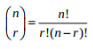
Or using the rows and terms from pascal's triangle below.
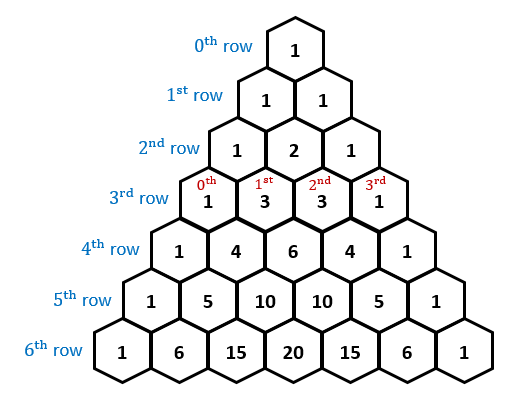
Since you are looking for an expansion to the power of four and the second term in that expansion, you look at row four and term 2. Therefore, your coefficient is 4.
(ignore for now the fact that the triangle says 0th term then 1st term- treat it like it begins with the 1st term from left to right)
To calculate the exponents on x and y:
According to the equation at the top of this explanation, y is to the power of n-1
Therefore y^3
And (-x) is to the power of 1
Therefore, just -x
(don't forget the minus! It is included as part of the x)
so the final second term expanded is:
-4(y^3)(x)
One way to think of it is that the coefficients come from Pascal's triangle, and the exponent for y decreases by one as you progress along the expansion, and the exponent for (-x) increases by one as you progress right along the expansion.
Example: