Question

How do use the binomial theorem to calculate `""^8C_5`?

Answer 1

`color(white)(A)^8C_5=56`

Explanation:

`color(white)(a)^nC_r=(n!)/(r!(n-r)!`

so

`color(white)(A)^8C_5=(8!)/(5!(8-5)!)`

`=(8xx7xx6xxcancel(5!))/(cancel(5!)3!)`

`=(8xx7xxcancel(6))/(cancel(3!))`

`=56`

Answer 2

`56`

Explanation:

`"using the definition of "^nC_r`

`•color(white)(x)^nC_r=(n!)/(r!(n-r)!)`

`"where "n! =n(n-1)(n-2)(n-3)......xx3xx2xx1`

`rArr^8C_5`

`=(8!)/(5!3!`

`=(8xx7xx6xxcancel(5xx4xx3))/(cancel(5!)xx3xx2xx1`

`=(8xx7xx6)/6=56`

Answer 3

`""^8C_5 = 56`

Explanation:

This seems a curious question to me, since normally you would use `""^8C_5 = (8!)/(3!5!)` to find a binomial coefficient, but let's give it a try.

Applying the Binomial theorem to `f(x) = (x+1)^8` we have:

`(x+1)^8 = ""^8C_0 x^8 + ""^8C_1 x^7 + ""^8C_2 x^6 + ""^8C_3 x^5 + ""^8C_4 x^4 + ""^8C_5 x^3 + ""^8C_6 x^2 + ""^8C_7 x + ""^8C_8`

Taking the derivative `3` times, we find:

`8 * 7 * 6 (x+1)^5`

`= f^((3)) (x)`

`= 8 * 7 * 6 * ""^8C_0 x^5 + 7 * 6 * 5 * ""^8C_1 x^4 + 6 * 5 * 4 * ""^8C_2 x^3 + 5 * 4 * 3 * ""^8C_3 x^2 + 4 * 3 * 2 * ""^8C_4 x + 3 * 2 * 1 * ""^8C_5`

So:

`8 * 7 * 6`

`= 8 * 7 * 6 * ((color(blue)(0))+1)^5`

`= f^((3)) (0)`

`= 8 * 7 * 6 * ""^8C_0 (color(blue)(0))^5 + 7 * 6 * 5 * ""^8C_1 (color(blue)(0))^4 + 6 * 5 * 4 * ""^8C_2 (color(blue)(0))^3 + 5 * 4 * 3 * ""^8C_3 (color(blue)(0))^2 + 4 * 3 * 2 * ""^8C_4 (color(blue)(0)) + 3 * 2 * 1 * ""^8C_5`

`= 3 * 2 * 1 * ""^8C_5`

So:

`""^8C_5 = (8 * 7 * 6) / (3 * 2 * 1) = 56`

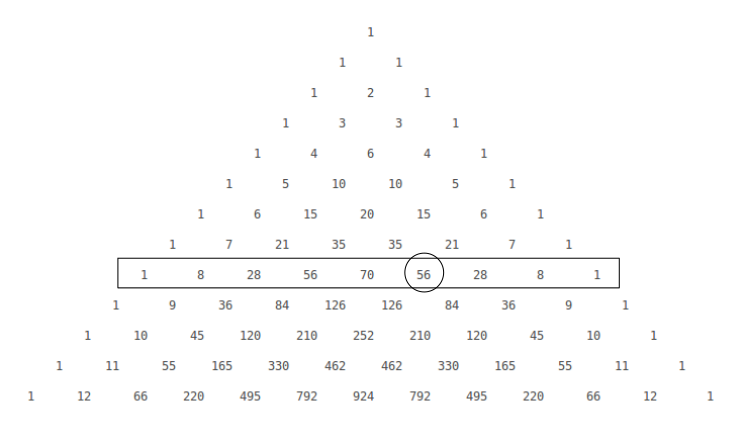
Alternatively, you might recognise that the method of constructing Pascal's triangle relates precisely to the values of the coefficients of `(a+b)^n` and hence deduce that the appropriate entry in Pascal's triangle must be the binomial coefficient.

The row of Pascal's triangle starting `1, 8,...` contains the coefficients for `(a+b)^8`, with the coefficient of `a^3b^5` being `56`, a.k.a. `""^8C_5` ...