How do you graph #f(x)=2^(x-1)-3# and state the domain and range?

Question

2876 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-02-03T14:27:36

Domain: #(-oo, oo)#

Range: #f(x)>(-3)#

Given:

#color(blue)(y = f(x) =2^(x-1)-3)#

Refer to the graph below to understand the behavior of the given exponential function:

graph{2^(x-1)-3 [-10, 10, -5, 5]}

Let us look at the table given below:

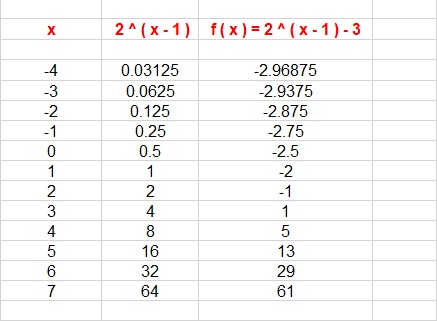
enter image source here

We observe that the domain will be all real values.

For every value of #x# there is a corresponding #y# value.

Hence

Domain: # (-oo, oo)#

Below you find a representation of both the parent function #color(green)(y=2^x and y = 2^(x-1)-3#

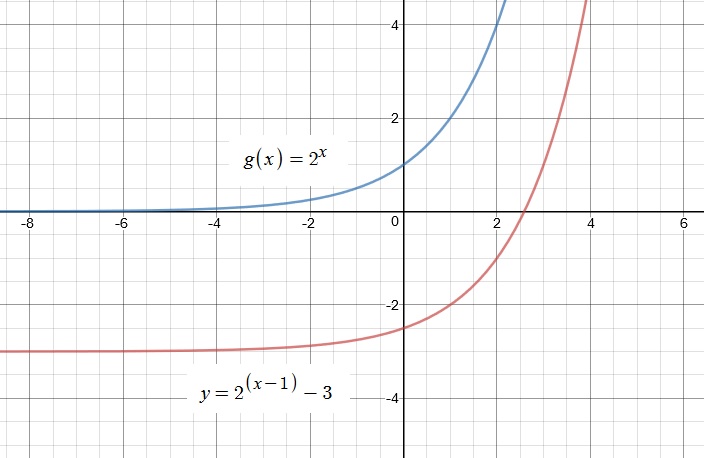
enter image source here

We find a horizontal asymptote at #y=-3#

Hence Range: #f(x)>(-3)#