Question

How do I show that `f(x)=0` has one root, when `f(x)= x^3-x^2+x-6`? 4 marks

Answer 1

`"See explanation"`

Explanation:

`"Use "underline("Descartes' rule of signs")" for positive real roots :"`
`f(x) = x^3 - x^2 + x - 6`
`"has 3 sign changes so there are 1 or 3 positive real roots"`

`"( Then use Descartes' rule of signs for negative real roots :"`
`f(-x) = -x^3 - x^2 - x - 6`
`"has no sign changes so there are no negative real roots.)"`

`"So there is at least one positive real root, and no negative real"`
`"roots."`

Answer 2

Show that `f(x)=x^3-x^2+x-6` has no critical points and therefore can not cross the X-axis more than once.

Explanation:

We know that, because of the `x^3` term
`f(x)=x^3-x^2+x-6` is negative for large magnitude, negative values of `x`
`color(white)("xxxxxxxxxxxxxxxx")`and positive for large magnitude, positive values of `x`.

If `f(x)` is to cross the X-axis more than once, it must have points where its slope changes from increasing to decreasing in order to "double back" and recross the X-axis.

Changes from increasing to decreasing slopes imply that at any such point the slope of the function must be zero;
in this case: `f'(x)=3x^2-2x+1` must be equal to zero.

The determinant of this: `(b^2-4ac)` in standard notation must be `>=0` for any such Real point to exist;
however in this case, the determinant `=(-2)^2-(4 * 3 * 1) < 0`
so there is no such "turning" (aka "critical") point.

Therefore the function can only cross the X-axis once.

As a help in verification, here is a graph of the original function `f(x)=x^3-x^2+x-6`:

Answer 3

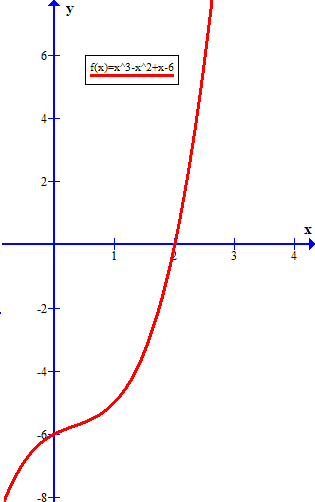
You can use the discriminant...

Explanation:

Given:

`f(x) = x^3-x^2+x-6`

The discriminant `Delta` of a cubic polynomial in the form `ax^3+bx^2+cx+d` is given by the formula:

`Delta = b^2c^2-4ac^3-4b^3d-27a^2d^2+18abcd`

In our example, `a=1`, `b=-1`, `c=1` and `d=-6`, so we find:

`Delta = 1-4-24-972+108 = -891`

Since `Delta < 0` this cubic has `1` Real zero and `2` non-Real Complex zeros, which are Complex conjugates of one another.

For the discriminant `Delta` of a cubic polynomial we have:

`Delta > 0` means that the cubic has `3` real zeros.

`Delta = 0` means that the cubic has a repeated real zero, which may be of multiplicity `3` or `2`. If multiplicity `2` then the third zero is also real.

`Delta < 0` means that the cubic has one real zero and a complex conjugate pair of non-real zeros.

Answer 4

There are several ways to answer this question. Concentrate on the one that looks most like what you've been studying.

Explanation:

Use the Intermediate Value Theorem to show that there is at least one root.

Use Rolle's or the Mean Value Theorem to show that there cannot be two roots.

Conclude that there is exactly one root.