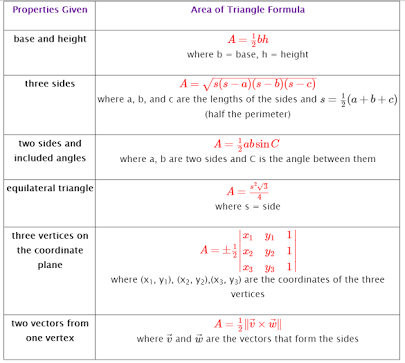
From the table above, having known three sides, we can find the area of the triangle using semi perimeter formula,
#A_t sqrt(s (s-f) (s-g) (s - h))# where s is the semi perimeter of the triangle and
#s = (a + b + c) / 2 = (10 + 11 + 4) / 2 = 12.5#
#A_t = sqrt(12.5 * (12.5-10) * (12.5 - 11) * (12.5 - 4)) ~~ color(brown)(20)#
But we know, #A_t = (1/2) f g sin (hatH)#
#:. sin H = (2 * A_t) / (f * g) = (2*20) /(10*11) = 0.3636#
#hatH = sin^-1 (0.3636) ~~ 0.3721^c#
#sin hatG = (g * sin hatH) / g = (11 * 0.3636) / 4 = 1#
#hat G = sin^(-1) 1 = 90^@ or pi/2^c or 1.57^c#
#hat F = pi - 0.3721 - (pi/2) = 1.1987^c#
It’s a right triangle.


