How do you find the equations for the tangent to the curve in the point [-1,-2]?
#x^2y^2=4#
3 Answers
Explanation:
Differentiate the equation implicitly:
For
The general equation of the tangent line in the point
that is, based on
and for
You can do it like this:
Explanation:
Using The Product Rule:
Differentiating implicitly:
This gives the gradient m of the tangent line:
The tangent line is of the form:
So the equation of the tangent line is:
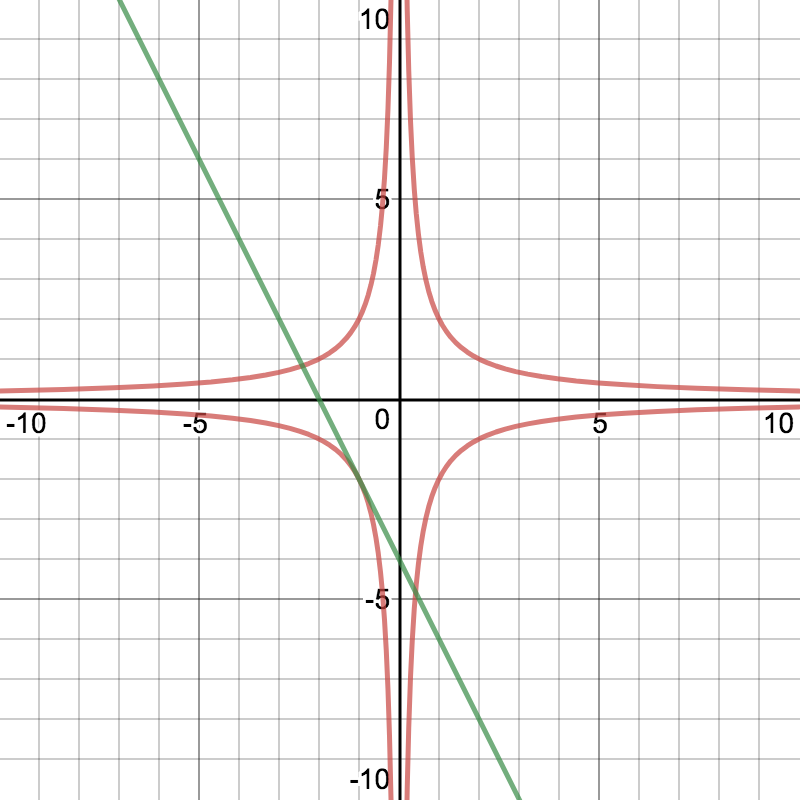
The functions look like this:
graph{(x^2y^2-4)(-2x-4-y)=0 [-10, 10, -5, 5]}
Explanation:
#"differentiate "color(blue)"implicitly with respect to x"#
#"differentiate "x^2y^2" using the "color(blue)"product rule"#
#•color(white)(x)m_(color(red)"tangent")=dy/dx" at "(-1,-2)#
#rArr(x^2 .2ydy/dx+2xy^2)=0#
#rArr2x^2ydy/dx=-2xy^2#
#rArrdy/dx=(-2xy^2)/(2x^2y)=-y/x#
#dy/dx" at "(-1,-2)=-(-2)/(-1)=-2#
#rArry+2=-2(x+1)#
#rArry=-2x-4larrcolor(red)"equation of tangent"#
graph{(x^2y^2-4)(y+2x+4)=0 [-20, 20, -10, 10]}


