Question

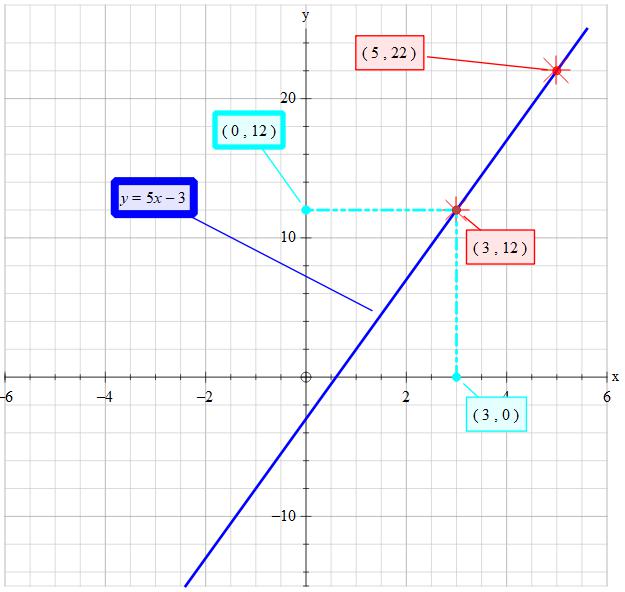
How do you write an equation in standard form for a line passing through (5,22) and (3,12)?

Answer 1

Use the points to write the equation in slope-intercept form.
Then write that equation in standard form.

Standard form for these points is

`color(white)(.....)` `5x - y = 3`

Explanation:

To write an equation in standard form when you have two points, first write the equation in slope-intercept form.

`"Write the equation in slope-intercept form"`
`color(white)(........)` `y = mx + b`

`color(white)(.........)`―――――――

First find `m`, the slope

Slope = `((y - y'))/((x - x'))`

1) Decide which point will be `(x,y)`

Assign `(5,22)` to be `(x,y)`
Assign `(3,12)` to be `(x',y')`

You can choose either point to be `(x',y')` and it will come out the same, but if you select wisely, you can sometimes avoid working with negative numbers.

2) Sub in the values for the variables

`((y - y'))/((x - x'))`

`((22 - 12))/((5 - 3))`

3) Do the subtractions to find the slope `m`

`color(white)(.....)` `(10)/(2)` `=5` `larr` value for slope `m`

4) So now the equation so far is

`color(white)(.....)` `y = 5x + b`

`color(white)(.........)`―――――――

Next find `b`, the y intercept

1) Using either given point, sub in the values for `(x,y)` and solve for `b`

`color(white)(.......)` `y = 5  x  + b`
`color(white)(.....)` `12 = 5(3) + b`

2) Clear the parentheses
`12 = 15 + b`

3) Subtract `15` from both sides to isolate `b`
`-3 = b`

So the equation in point-slope form is
`color(white)(.....)` `y = 5x - 3`

`color(white)(.........)`―――――――

Now put the equation in standard form

`color(white)(.......)` `ax + by = c`
where `a` is a positive integer

`color(white)(.....)` `y = 5x - 3`

1) Subtract `5x` from both sides to isolate the constant

`-5x + y = - 3`

2) Multiply through by `-1` to clear the minus sign on `x`

`5x - y = 3` `larr` standard form

Answer 2

`5x-y=3` same as `y=5x-3`

Explanation:

`color(blue)("Preamble")`

Gradient (slope) is:

`m=(y-("known value for "y))/(x-("known value of "x)) ..Equation(1)`

Method
Step 1: determine `m` from the given points.
Step 2: use one of the given points to substitute values for `x and y` into `Equation(1)`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Answering the question")`

`color(brown)("Step 1:")`

Always read left to right on the x-axis for this:

Set the left most point as `P_1->(x_1,y_1)=(3,12)`
Set the rightmost point as `P_2->(x_2,y_2)=(5,22)`

Set the gradient (slope) as `m`

`m=("change in the y-axis")/("change in the x-axis") ->(y_2-y_1)/(x_2-x_1)=(22-12)/(5-3)=10/2`

But `10/2` is the same as `5/1->5`

`m=5/1 larr" Deliberately written this way"`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(brown)("Step 2:")`

Using `P_1`

`m=("change in the y-axis")/("change in the x-axis")->m=5/1=(y-12)/(x-3)`

Cross multiply giving:

`5(x-3)=1(y-12)`

`5x-15=y-12`

`5x-y=15-12`

`5x-y=3`