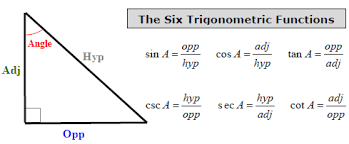
How do you find the measure of each of the angles of a triangle given the measurements of the sides are 7, 24, 25?

Question

19254 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-09T01:43:42

#color(green)(hat A = 16.26^@, hat B = 73.74^@, hat C = 90^@#

Pythagoras' theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle.

It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides

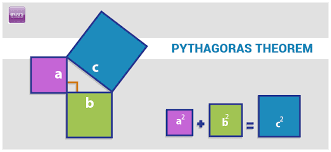
Given #a = 7, b = 24, c = 25#

#a^2 + b^2 = 7^2 + 24^2 = 625 = c^#

Hence it's a right triangle with #hat C = pi/2 = 90^@#

#sin A = (opp)/ (hyp) = b/c = 7 / 25 #

#hat A = sin^-1 (7/25) = 0.2838^c or 16.26^@#

#:. hat B = pi - pi/2 - 0.2838 = 1.287^c or = 73.74^@#

#color(red)("Verification : ")sin B = ( opp) / (hyp) = 24 / 25#

#hat B = sin ^-1(24/25) = 1.287^c or = 73.74^@#