Question

How do you write an equation in standard form if the line passes through (3,7) and (0, -2)?

Answer 1

`3x - y = 2`

Explanation:

We have the value of two points, `(3, 7)` and `(0, -2)`

First, let's find the slope of this line. The formula for slope is `"rise"/"run"` or `"change in y"/"change in x"` or `(y_2-y_1)/(x_2-x_1)`.

Since we have the values of two points, we can plug them into the formula:
`(-2-7)/(0-3)`

Simplify:
`(-9)/-3`

The negatives cancel out and we simplify it:
`3`

Now we can write the equation in point-slope form, shown here:

`y - 7 = 3(x-3)`

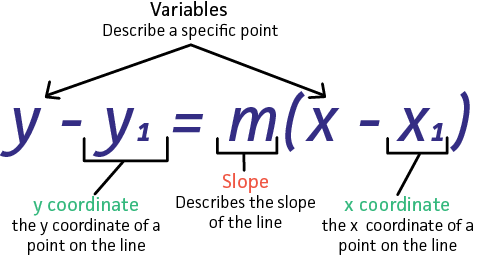
To convert to standard form, we first have to convert from point-slope to slope-intercept form, shown here:

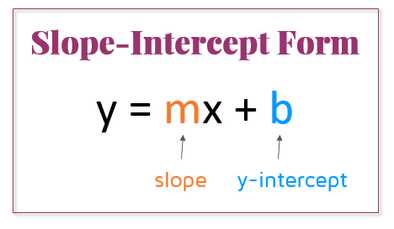
So let's simplify:
`y - 7 = 3x - 9`

Add `7` on both sides of the equation:
`y - 7 quadcolor(red)(+quad7) = 3x - 9 quadcolor(red)(+quad7)`

`y = 3x -2`

It is now in slope-intercept form.

Now let's convert this to standard form, by making the `y`-intercept by itself, shown here:

`y = 3x - 2`

Add `2` to both sides of the equation:
`y quadcolor(red)(+quad2) = 3x - 2 quadcolor(red)(+quad2)`

`y + 2 = 3x`

Subtract `y` on both sides of the equation:
`y + 2 quadcolor(red)(-quady) = 3x quadcolor(red)(-quady)`

`2 = 3x - y`

Switch sides to put in exact standard form:
`3x - y = 2`

As you can see, it is now in standard form.

For more information on writing an equation in standard form from two points, feel free to watch these videos:

Short video:

Longer video:

Hope this helps!