Question

How do you graph `f(x)=3^(x - 2)`?

Answer 1

`" "`
Please read the explanation.

Explanation:

`" "`
Given the exponential function: `color(red)(f(x)=3^(x-2)`

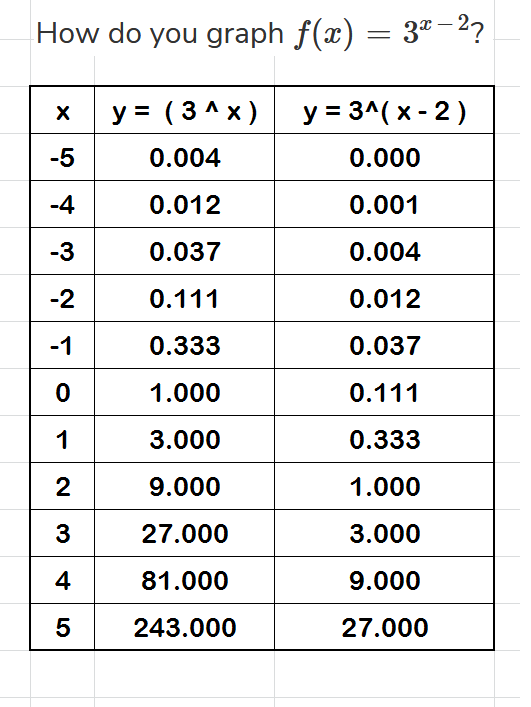
Before graphing this function, create a data table:

The table should contain values for `color(red)(x`, corresponding values for `color(red)(y=3^x) and color(red)(y=3^(x-2)`

We include the base function: `color(red)(y=3^x`, since it provides an opportunity to examine the behavior of both the graphs by comparing them.

The table shows `color(red)x` and the corresponding `color(red)(y` values:

Construct both the graphs:

`color(green)"Graph 1:"`

`color(blue)("Graph of "y = f(x) = 3^x`

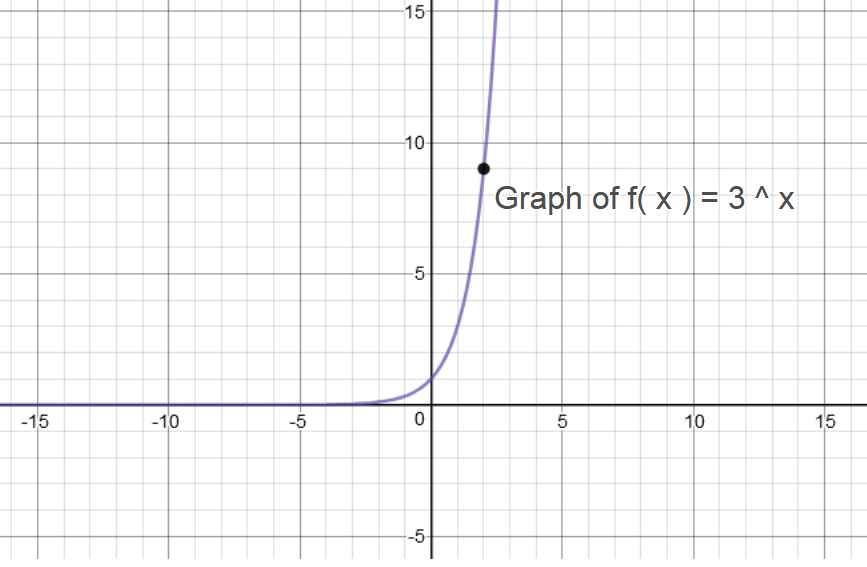
Domain : `(-oo, oo)`

Range : `(0, oo)`

y-intercept : `(0,1)`

Horizontal Asymptote :`y=0`

`color(green)"Graph 2:"`

`color(blue)("Graph of "y = f(x) = 3^(x-2`

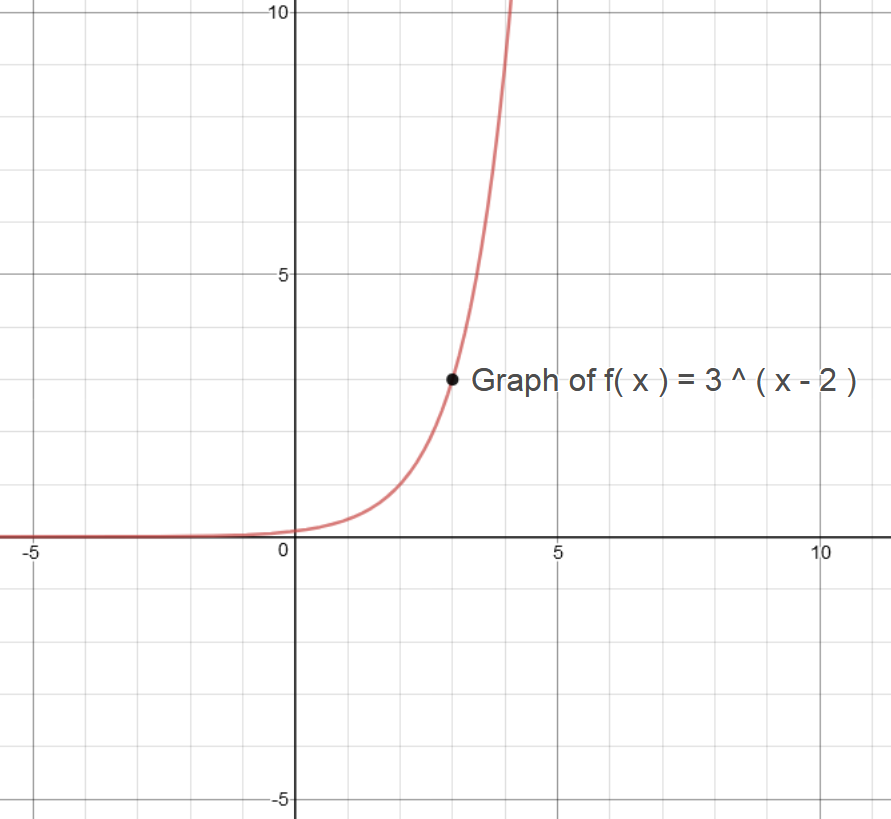
Domain : `(-oo, oo)`

Range : `(0, oo)`

y-intercept : `(0,1/0)`

Horizontal Asymptote :`y=0`

`color(green)"Graph 3:"`

`color(blue)("Graph of "y = f(x) = 3^(x) and y = f(x) = 3^(x-2)`

Compare the behavior of both graphs:

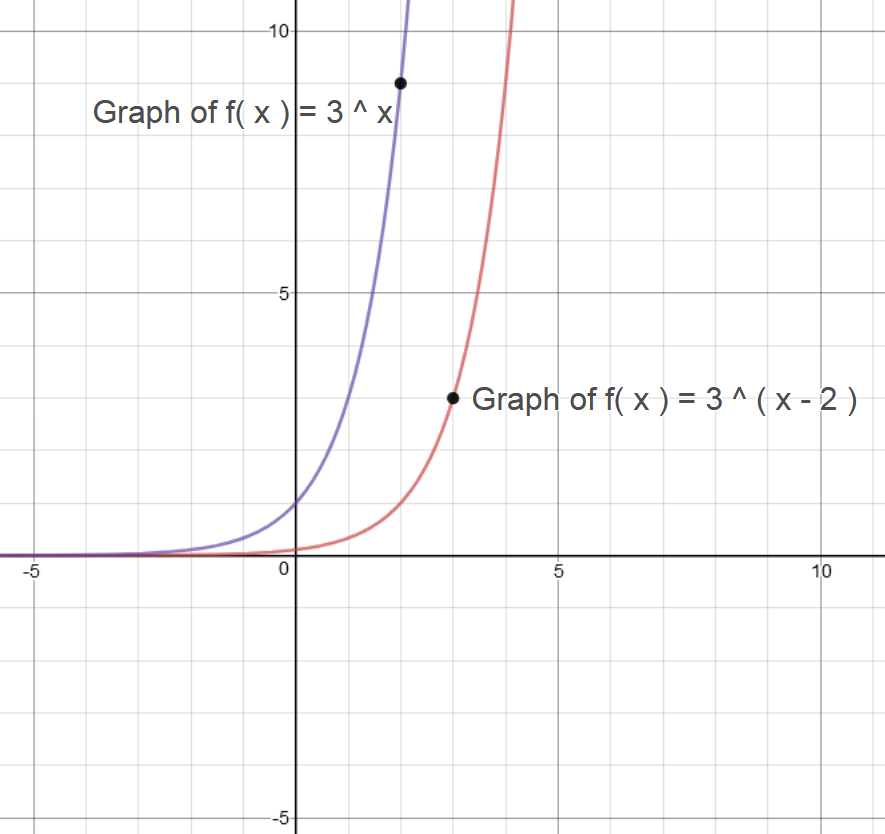
Translation is horizontal for `y = f(x) = 3^(x-2)` by `color(red)(2` units.

Hope it helps.