Given a triangle with sides measuring 15in, 10in, and 12in; with angle C across from 10in, angle A across from 12in, and angle T across from 15in. How do you find the angle measures?

Question

3516 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-05-05T03:23:53

#color(maroon)("Measure of Angles " color(indigo)(hat A = 52.89^@, hat C = 41.62^@, hat T = 85.49^@#

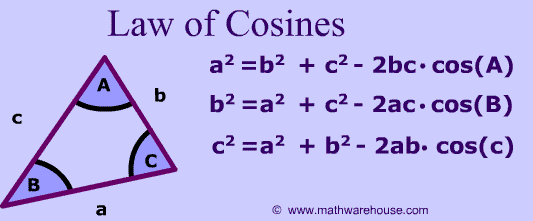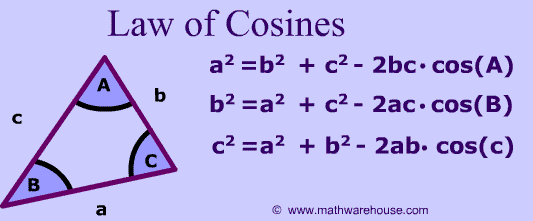
#"Given : " a = 12 " in", c = 10 " in", t = 15 " in"#

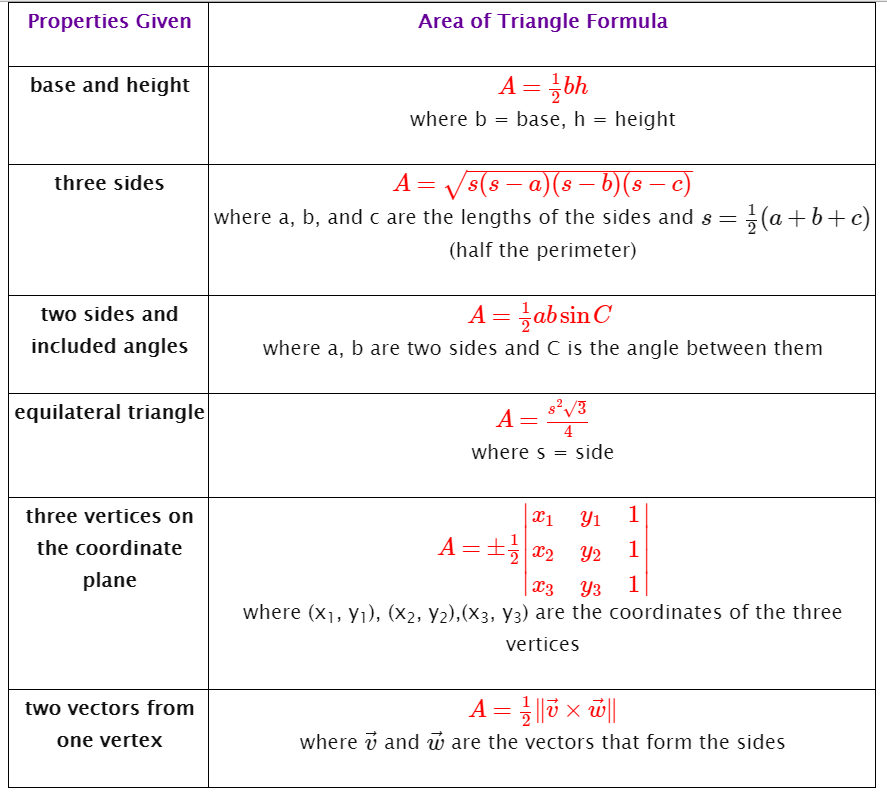
#color(green)("Knowing three sides of a triangle, we can use Heron's formula to calculate the area."#

#s = (a + c + t) / 2 = (12 + 10 + 15) / 2 = 18.5#

#A_t = sqrt(18.5 * (18.5-12) * (18.5 - 10) * (18.5 - 3)) = 59.8 " in"^2#

#color(crimson)("Using two sides and included angle to find area"#,

#A_t = (1/2) * a * c * sin T#

#sin T = (2 * 59.8) / (12 * 10) = 0.9969#

#hat T = sin ^-1 0.9969 ~~ 85.49@#

#color(maroon)("Using Law of Sines"#

#a / sin A = c / sin C = t / sin T#

#12 / sin A = 10 / sin C = 15 / sin (85.49^@)#

#sin A = (12 * sin (85.49) ) / 15 = 0.7975#

#hat A = sin ^-1 0.7975 = 52.89^@#

#hat C = 180 - hat A - hat T = 180 - 85.49 - 52.89 = 41.62^@#

Answer 2 · 2018-05-05T03:37:46

#color(indigo)(hat A = 53.13@, hat C = 41.65@, hat T = 85.22@#

#a = 12, c = 10, t = 15#

#cos A = (c^2 + t^2 - a^2) / (2 c t)#

#cos A = (10^2 + 15^2 - 12^2) / (2 * 10 * 15) = 0.6#

#hat A = cos ^ -1 0.6 = 53.13@#

#cos C = (a^2 + t^2 - c^2) / (2 a t)#

#cos C = (12^2 + 15^2 - 10^2) / (2 * 12 * 15) = 0.7472#

#hat C = cos ^ -1 0.7472 = 41.65@#

#hat T = 180 - hat A - hat C = 180 - 53.13 - 41.65 = 85.22@#