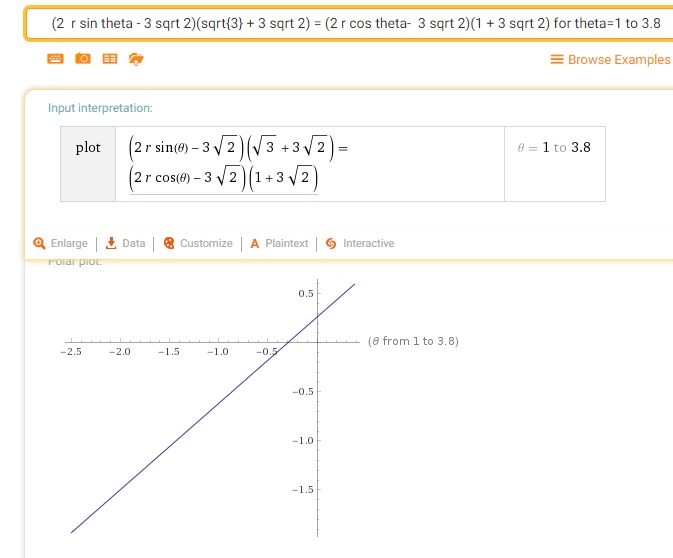
How do you write the polar form of the equation of the line that passes through the points #(3,pi/4)# and #(2,(7pi)/6)#?

Question

3914 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-05-05T06:52:16

# (2 r sin theta - 3 sqrt 2)(sqrt{3} + 3 sqrt 2) = (2 r cos theta- 3 sqrt 2)(1 + 3 sqrt 2) #

I have to keep pointing out that most trig only uses two triangles. This is another 45/45/90 and 30/60/90 problem.

A line through rectangular coordinates #(x_1, y_1)# and #(x_2,y_2)# looks like

# (y - y_1)(x_2 - x_1) = (x - x_1)(y_2 - y_1)#

#x = r cos theta#

#y = r sin theta#

# x_1 = 3 cos(pi/4) = 3/2 sqrt 2#

#y_1 = 3 sin( pi/4) = 3/2 sqrt 2#

#x_2 = 2 cos ({7pi}/6) = -sqrt{3}/2 #

#y_2 = 2 sin({7 pi}/6)=-1/2#

# ( r sin theta - 3/2 sqrt 2)(-sqrt{3}/2 - 3/2 sqrt 2) = (r cos theta- 3/2 sqrt 2)(-1/2 - 3/2 sqrt 2)#

We could stop here but let's clear the fractions and a minus sign.

# (2 r sin theta - 3 sqrt 2)(sqrt{3} + 3 sqrt 2) = (2 r cos theta- 3 sqrt 2)(1 + 3 sqrt 2) #

Check: Alpha

enter image source here