How do you solve #sqrt(2x+8) = x#?
2 Answers
x=4
Explanation:
to get rid of the square root on the right you square both sides so
Then bring
now you can do the quadratic formula to find the zeroes
Explanation:
#color(blue)"square both sides"#
#"note that "sqrtaxxsqrta=(sqrta)^2=a#
#rArr2x+8=x^2#
#"rearrange into "color(blue)"standard form ";ax^2+bx+c=0#
#"subtract "2x+8" from both sides"#
#0=x^2-2x-8#
#"the factors of - 8 which sum to - 2 are - 4 and + 2"#
#rArr0=(x-4)(x+2)#
#"equate each factor to zero and solve for x"#
#x+2=0rArrx=-2#
#x-4=0rArrx=4#
#color(blue)"As a check"# Substitute these values into the left side of the equation and if equal to the right side then they are the solution.
#x=-2tosqrt(-4+8)=sqrt4=2!=-2#
#rArrx=-2" is an extraneous solution"#
#x=4tosqrt(8+8)=sqrt16=4=" right side"#
#rArrx=4" is the solution"#
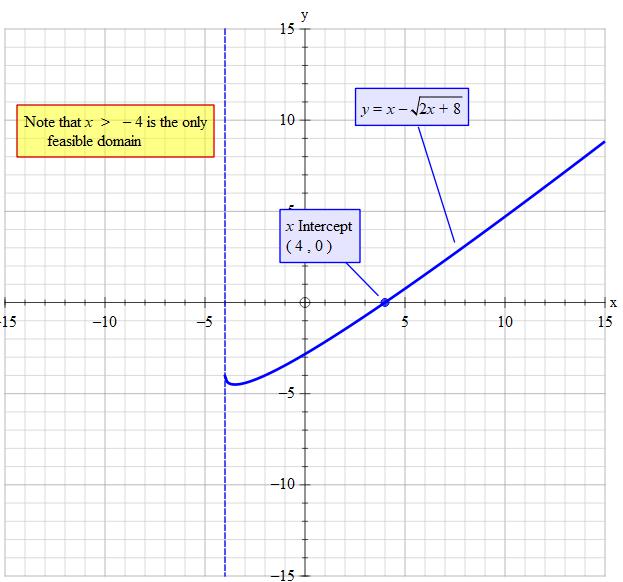
If you plot it as