How do you solve # -2x^2-6=0# graphically?

Question

1777 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-05-10T13:57:38

#" "#
Please read the explanation.

#" "#
#color(green)"Step 1:"#

#"Given: "y = -2x^2-6=0#

Create a data table for #y=f(x) = -2x^2-6#

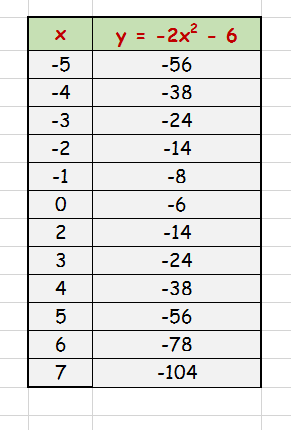
enter image source here

Plot the points and graph:

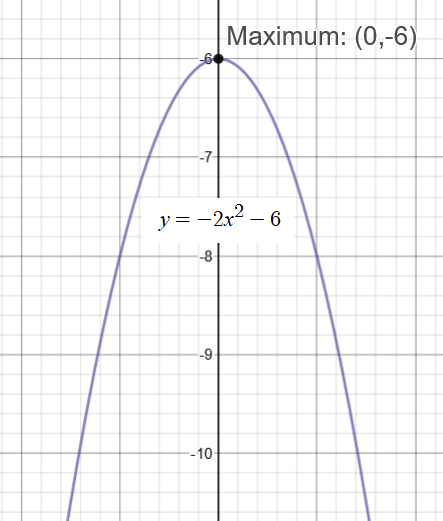
enter image source here

#color(green)"Step 2:"#

Observations:

The graph of this quadratic function shows that there are no real roots (zeros) because the graph does not cross the x-axis.

Such a graph tells us that the roots of the equation are complex numbers, and will appear in the #"form " a + bi. #

Roots that possess this pattern are called complex conjugates or, in general, conjugate pairs).

#"Vertex: Maximum at" (0,-6)#

#"Axis of Symmetry: " x=0#

Hope it helps.