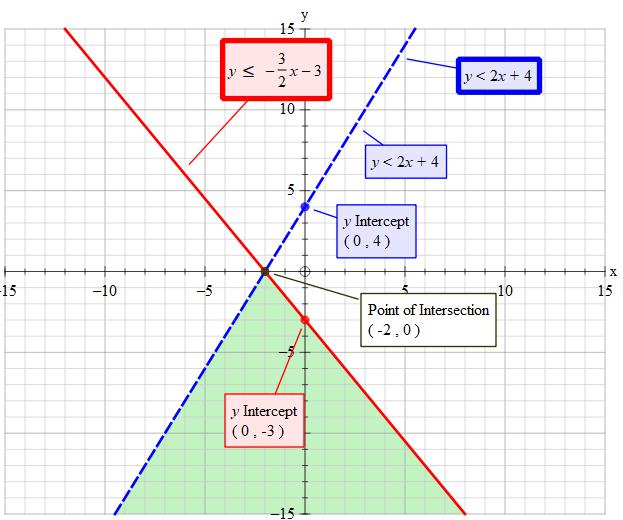
Given:
#y<2x+4" ".......................Eqn(1)#
#-3x-2y>=6" ".....................Eqn(2)#
#color(blue)("Converting "Eqn(2)" into standardised form ")#
Consider #Eqn(2)#
Add #2y# to both sides and subtract #6# from both sides giving:
#-3x-6>=2y#
Divide both sides by 2
#-3/2 x-6/2>=y#
Write the order as per convention
#y<=-3/2x-3" "..........Eqn(2_a)#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Plot them #color(magenta)(ul("as if they were"))#
#y=-3/2 x-3 color(white)("dddd") ->color(white)("dddd")"really is: " y<2x+4 " "Eqn(2_a)#
Feasible solution area is below #color(white)()"and "ul(color(red)("including the solid line"))color(white)("d") Eqn(2_a)#
and:
#y=2x+4 color(white)("dddd") ->color(white)("dddd")"really is: " y<2x+4" "Eqn(1)#
Feasible solution area is below and
#color(red)(ul("excluding the dotted line "))Eqn(1)#
The solution area is where these two are coincidental (coincide).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine key point - Intersection of the two lines")#
#y=2x+4 " "............Eqn(1)#
#y=-3/2 x-3" "......Eqn(2_a)#
#Eqn(1)-Eqn(2)# to 'get rid' of the # y's#
#0=7/2x+7#
#color(green)(x=-7xx2/7=-2)#
Substitute #x=-2# in #Eqn(2_a)# giving:
#y=(-3/2)(-2)-3 = +3-3=0#
#color(blue)(ul(bar(| color(white)(2/2) "Intersection"->(x,y)=(-2,0)color(white)(2/2) |))#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine key point - axis intercepts for "y<2x+4)#
Set #y=2x+4#
Set #x=0 ->
color(blue)(bar(ul(|color(white)(2/2)y_("intercept")=4color(white)(2/2)|))#
Set #y=0 -> color(blue)(ul(bar(|color(white)(2/2) x_("intercept")=-2color(white)(2/2)|))#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine key point - axis intercepts for "-3x-2y>=6)#
#Eqn(2_a)->y<=-3/2x-3#
Set #y=-3/2x-3#
Set # x=0 ->color(blue)( ul(bar(| color(white)(2/2)y_("intercept")= -3color(white)(2/2)|)))#
Set #y=0->color(blue)( ul(bar(| color(white)(2/2)x_("intercept")= -2color(white)(2/2)|)))#