A parallelogram has sides with lengths of #15 # and #12 #. If the parallelogram's area is #120 #, what is the length of its longest diagonal?

Question

1406 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-12T17:33:06

#color(blue)("Longest diagonal"=sqrt(369+120sqrt(5))~~637.3281572#

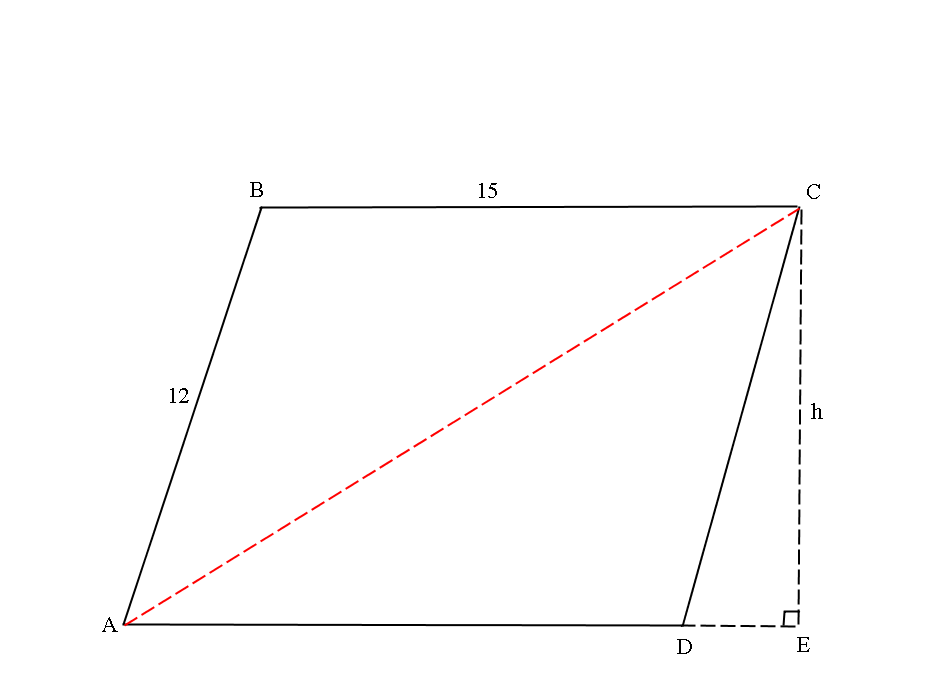
enter image source here

From the diagram, we need to find the diagonal AC.

Notice we can form a right angled #DeltaACE# of which #AC# is the hypotenuse.

We are given "area=120#

Area of a parallelogram is given by:

#"Area"="base"xx"height"#

#:.#

#120=15h=>h=8#

Using Pythagoras' theorem:

#DE=sqrt((CD)^2-h^2)#

#DE=sqrt(12^2-8^2)=sqrt(80)#

#AE=AD+DE=15+sqrt(80)#

Using Pythagoras' theorem again:

#(AC)^2=h^2+(AE)^2#

#(AC)^2=8^2+(15+sqrt(80))^2#

#AC=sqrt(369+120sqrt(5))~~637.3281572#