The base of a triangular pyramid is a triangle with corners at #(6 ,2 )#, #(3 ,8 )#, and #(4 ,4 )#. If the pyramid has a height of #6 #, what is the pyramid's volume?

Question

1644 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-19T02:46:26

#color(purple)("Area of " Delta = A_t = 3 " sq units"#

#"coordinates of three vertices are "#

#A(x,y) = 6,2), B(x,y) = (3,8), C(x,y) = (4,4)#

#a = sqrt ((3-4)^2 + (8-4)^2 = sqrt17 = 4.123#

#b = sqrt((4-6)^2 + (4-2)^2) = sqrt8 = 2.828#

#c = sqrt((6- 3)^2 + (2-8)^2) = sqrt45 = 6.708#

#"Semi-perimeter " = s = (a + b + c) / 2 #

#s = (4.123 + 2.828 + 6.708) / 2 = 6.83#

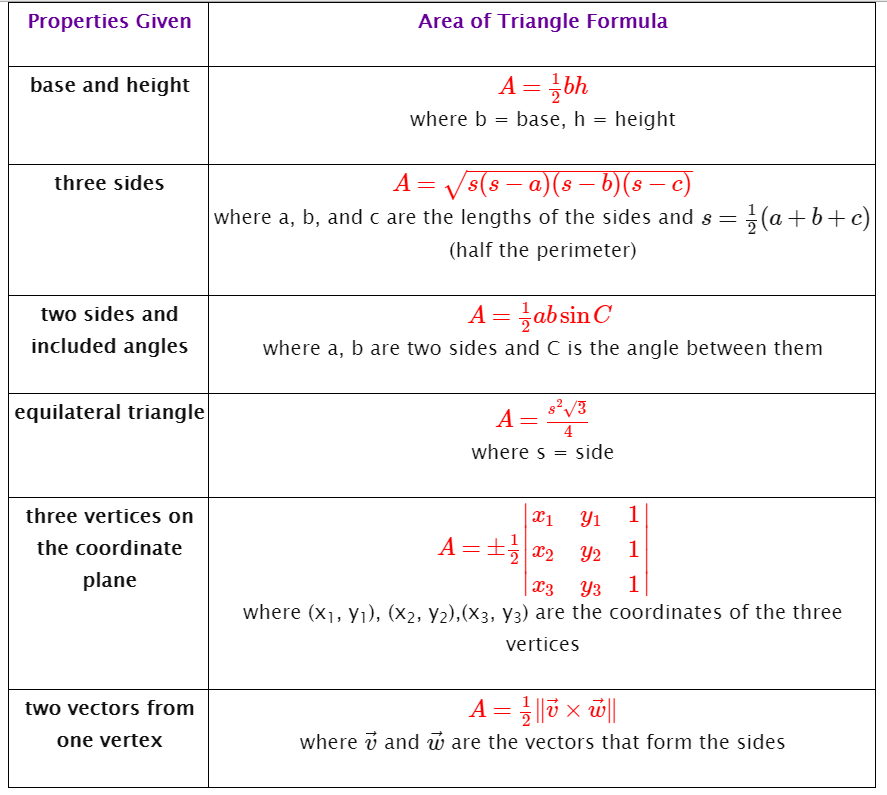
#"Area of " Delta = A_t = sqrt (s (s-a) (s-b) (s - c)), " using the formula from the above table, knowing three sides"#

#A_t = sqrt (6.83 * (6.83 - 4.123) (6.83 - 2.828) (6.83 - 6.708))#

#color(purple)("Area of " Delta = A_t = 3 " sq units"#