Question

How do you graph `f(x)=x^2-x+5/4` and identify the x intercepts, vertex?

Answer 1

`" "`
Vertex: `color(red)((0.5, 1)`

x-intercept: None.

Explanation:

`" "`
We are given the Quadratic equation:

`color(blue)(y=f(x)=x^2-x+5/4`

To draw a graph, create a table of values using the given quadratic function `color(red)(f(x)):`

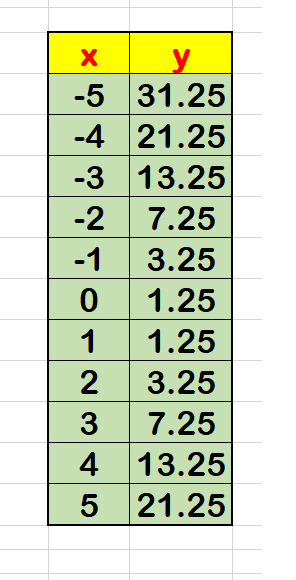
Using this table, plot the points and draw the graph:

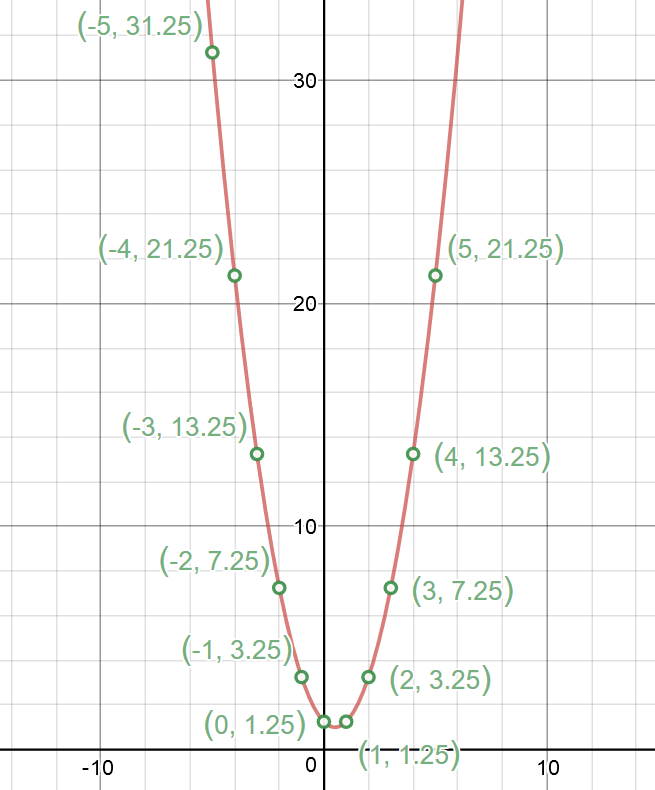
Since the coefficient of the `color(red)(x^2` term is positive, the graph (parabola) will open up and will have a minimum point:

Minimum Point is the Vertex of the Parabola:

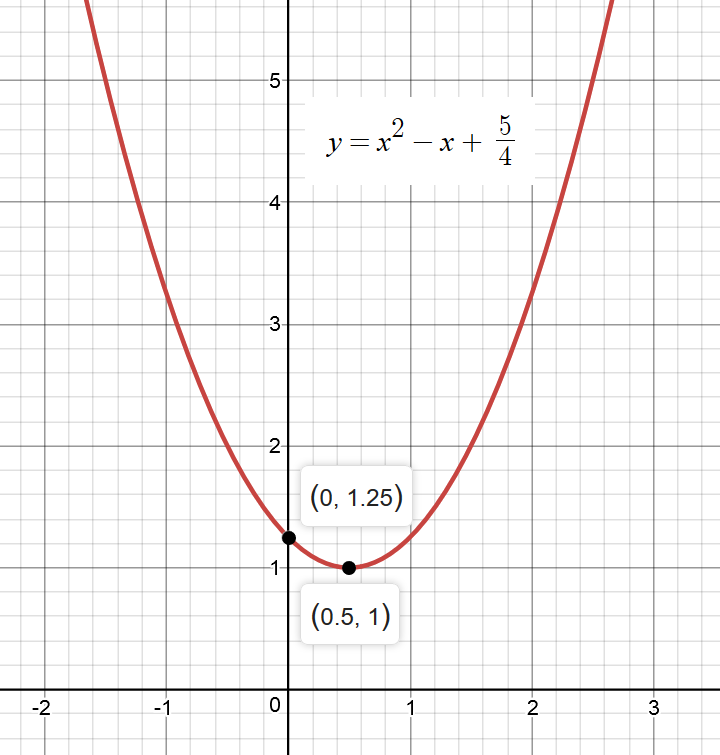
From the graph, it is obvious that Vertex (Minimum point) is at: `color(blue)(0.5,1)`

Since the parabola does not intersect the x-axis, the graph does not have an x-intercept.

The parabola passes through the y-axis.

So, y-intercept: : `color(red)(0,1.25)`