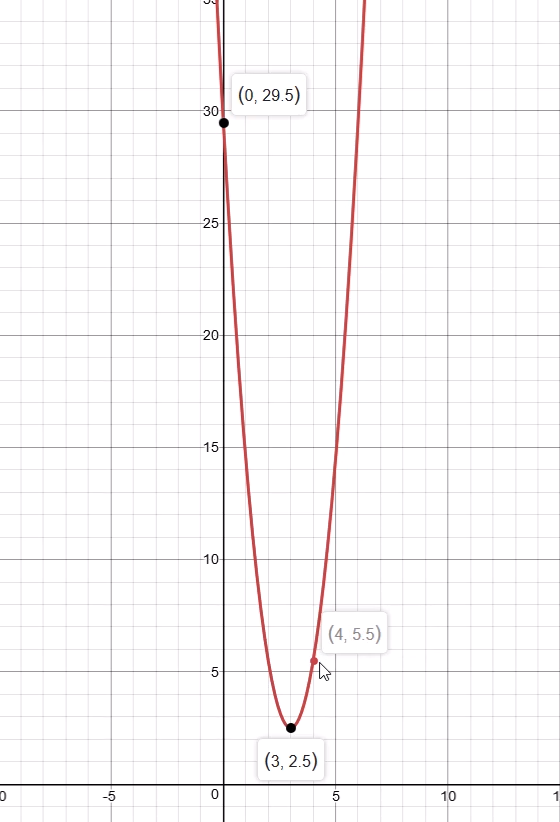
How do you write the vertex form of a parabola with (3,2.5) and (4,5.5)?

Question

1914 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-07-18T05:50:01

#y=3(x-3)^2+2.5#

Let us take #(3, 2.5)# the vertex and passes through the point #(4,5.5)#

#y=a(x-h)^2+k#

Where -

#h=3#
#k=2.5#

Then -

#y=a(x-3)^2+2.5#

To find the value of #k#, assume the parabola is passing through the point #(4, 5.5)#

Then -

#a(4-3)^2+2.5=5.5#

#a+2.5=5.5#

#a=5.5-2.5=3#

Plug in the value #a=3# in #y=a(x-3)^2+2.5#

#y=3(x-3)^2+2.5#

enter image source here