Question

How do you solve a linear inequality `3x + 2y < 6`?

Answer 1

`" "`
`color(red)(y<(6-3x)/2`

Explanation:

`" "`
We are given the inequality: `color(blue)(3x+2y<6`

`rArr 3x+2y<6`

Subtract `color(red)(3x` from both sides of the inequality.

`rArr 3x+2y -3x< 6-3x`

`rArr cancel(3x)+2y -cancel(3x)< 6-3x`

`rArr 2y< 6-3x`

Divide both sides of the inequality by `color(red)(2`

`rArr (2y)/2< (6-3x)/2`

`rArr (cancel 2y)/cancel 2< (6-3x)/2`

`rArr y<(6-3x)/2`

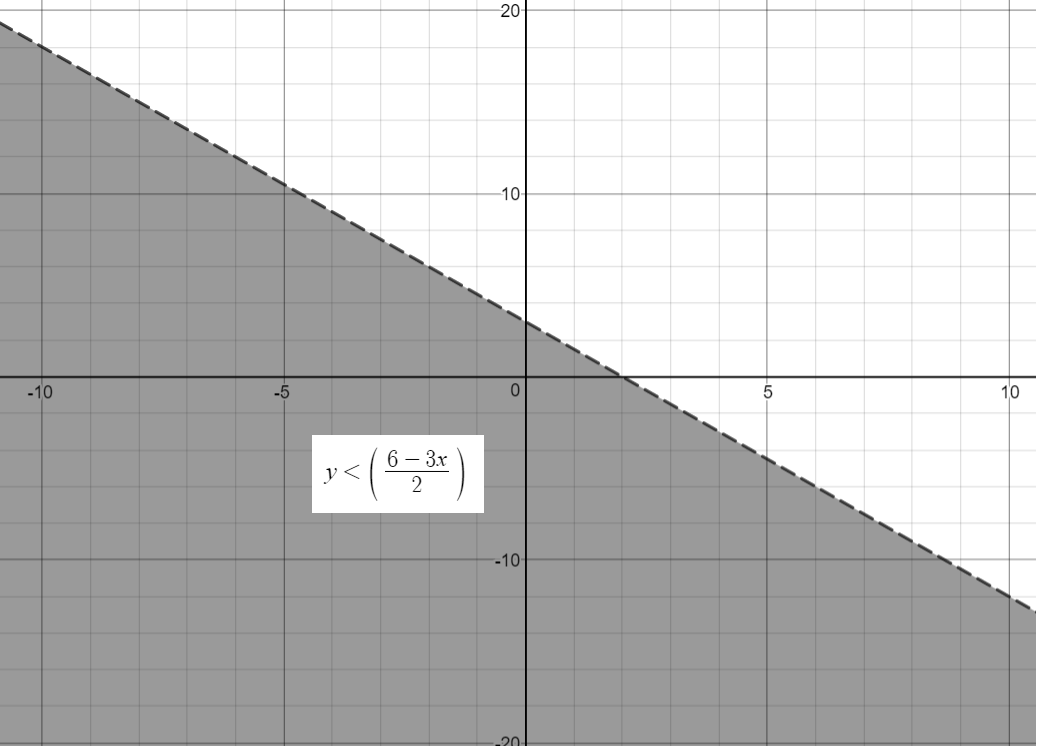
Hence, our final solution is given by:

`color(blue)(y<(6-3x)/2`

We can also graph this solution as given below:

Note that the dotted line in the graph indicates value that is NOT a part of the final solution.

Hope this helps.