Question

How do you graph and solve `2-x<=3-(5x-4)`?

Answer 1

`" "`
The given inequality

`color(red)(2-x<=3-(5x-4)`

can be simplified to

`color(blue)(x<=5/4`

Explanation:

`" "`
How do we graph and solve `color(red)(2-x<=3-(5x-4)` ?

We will try to simplify the inequality first before graphing:

`color(blue)(2-x<=3-(5x-4)`

Remove the parenthesis:

`rArr 2-x<= 3-5x+4`

Combining like terms and simplifying:

`rArr 2-x<= 7-5x`

Add `color(red)(5x` to both sides of the inequality:

`rArr 2-x+5x<= 7-5x+5x`

`rArr 2+4x<= 7-cancel (5x)+cancel (5x)`

Rearrange the terms and simplify:

`rArr 4x+2<=7`

Subtract `color(red)(2` from both sides of the inequality:

`rArr 4x+2-2<=7-2`

`rArr 4x+cancel 2-cancel 2<=7-2`

`rArr 4x<=5`

Divide both sides of the inequality by `color(red)(4`

`rArr 4x<=5`

`rArr (4x)/4<=5/4`

`rArr (cancel 4x)/cancel 4<=5/4`

`color(red)(x<=5/4`

This is our simplified inequality.

We can graph this inequality as shown below:

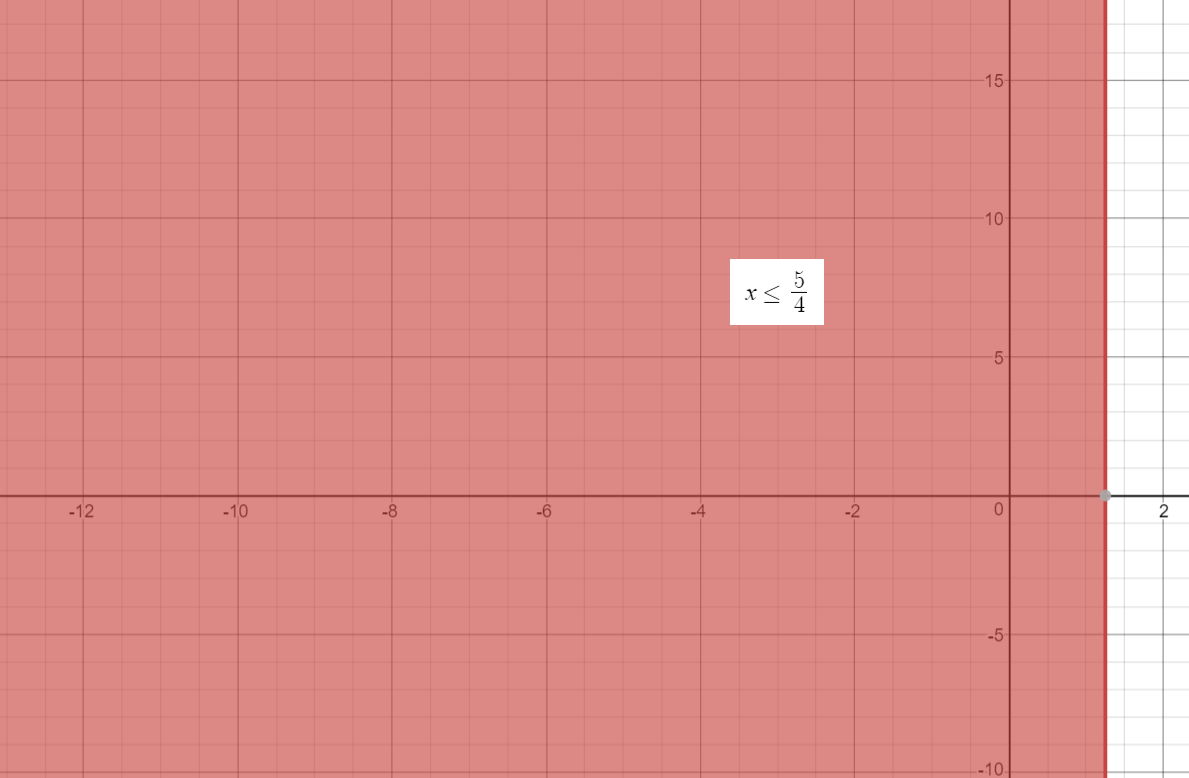
The solid line in the graph indicates the value `color(blue)([x=(5/4)]` that is part of the final solution.

Hope it helps.