Question

How do you identify the important parts of `y= -4x^2` to graph it?

Answer 1

`" "`
Please read the explanation.

Explanation:

`" "`
Vertex-Form of a Quadratic Equation:

`color(red)(y=f(x)=a(x-h)^2+k`, where

`color(red)((h,k)` is the Vertex

`y=f(x)=x^2`

is the parent function

We can see that `a=1; h=0,k=0`

Vertex `color(red)((0,0)`

Axis of Symmetry is at `color(red)((x=0)`

Since `a>0`, the parabola opens up.

For the given function:

`color(blue)(y=f(x)=-4x^2`

`a=-4, h=0, k-0`

The value of `color(red)(a, (a<0)`, the parabola opens down.

Vertex is at `color(red)((0,0)`

Axis of Symmetry is at `color(red)((x=0)`

Make a data table for the parent function

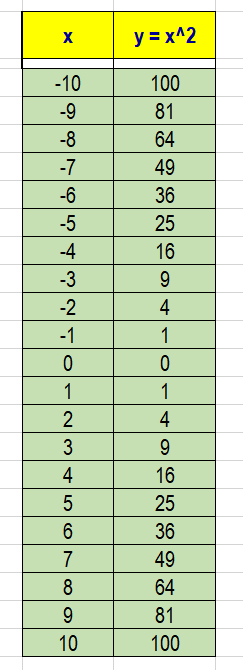
Make a data table for the given function

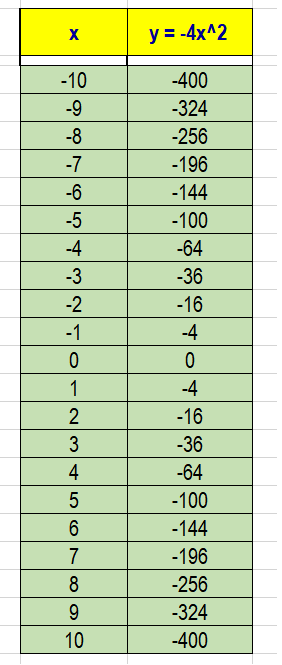
Draw the graphs for both of them and analyze the behavior of the quadratic functions:

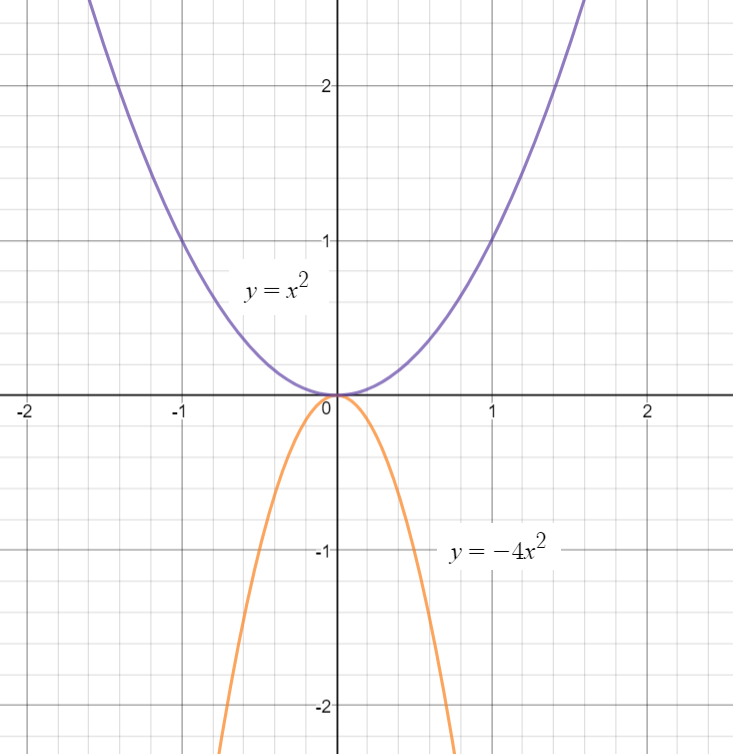
The graph of the given function

`color(blue)(y=f(x)=-4x^2`

is compressed horizontally since `a=-4`

Hope this is helpful;.