Drawing Atomic and Molecular Orbitals Diagrams for Molecules
Key Questions
-
A Lewis resonance structure is one structural "snapshot" out of many that contribute to a molecule or polyatomic ion's overall, real-life resonance hybrid structure.
Let us take
#"NO"_3^(-)# as an example. Noting that the total number of valence electrons is#5 + 6*3 + 1 = 24# (the last one due to its charge), and knowing that nitrogen commonly makes three bonds but a maximum of four bonds (more than oxygen can make), we can draw the following Lewis resonance structures:The resonance hybrid structure is actually
because in reality, the electrons in this polyatomic ion are delocalized, meaning that they travel freely throughout the system.
Because the electrons aren't fully localized as one
#"N"="O"# bond, nor are they fully localized somewhere else as one#"N"-"O"# bond, they are somewhere in between "single" and "double" bonds. So, we essentially have "one-and-one-half" bonds on average between each oxygen and the central nitrogen.The individual resonance structures simply illustrate still states for the electron distributions that contribute to the overall resonance hybrid.
-
I will use oxygen (
#"O"_2(g)# ) as an example.With oxygen, you know that the atomic orbital potential energies go in the following order:
#V_(1s)# #"<<"# #V_(2s) < V_(2p)# So the atomic orbital diagram is simply those orbitals in that order of energy. Note that the
#1s# orbitals are significantly lower in energy than the#2s# orbitals.For the homonuclear diatomic
#"O"_2# , we simply have two copies of this atomic orbital diagram far apart at first. Fill those with oxygen's 8 electrons (2 core + 6 valence).Now we have two of the same atomic orbital diagrams laid out:

Then, for the molecular orbital diagram, we examine how these atomic orbitals interact with each other in a linear combination of atomic orbitals (LCAO). Here's how this goes (of course, the
#ns# are compatible with the#ns# ).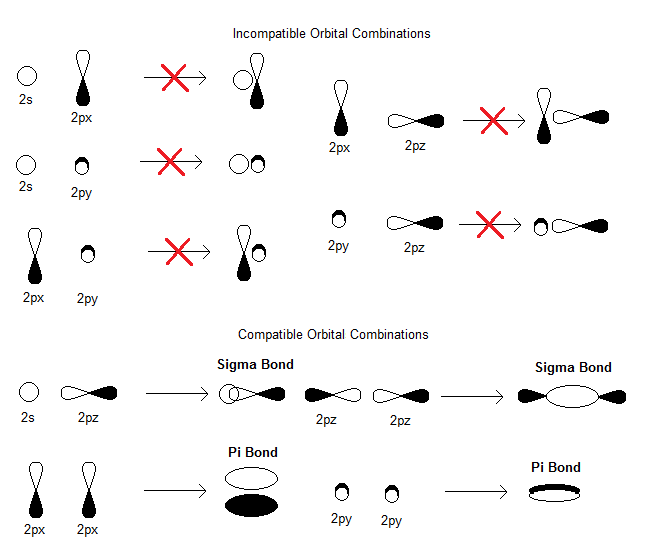
Taking the internuclear axis as the
#z# -axis, we have:#"AO"_(1s) + "AO"_(1s) = sigma_(1s) + sigma_(1s)^"*"# (strong head-on overlap)#"AO"_(2s) + "AO"_(2s) = sigma_(2s) + sigma_(2s)^"*"# (strong head-on overlap)#"AO"_(2p_x) + "AO"_(2p_x) = pi_(2p_x) + pi_(2p_x)^"*"# (weak sidelong overlap)#"AO"_(2p_y) + "AO"_(2p_y) = pi_(2p_y) + pi_(2p_y)^"*"# (weak sidelong overlap)#"AO"_(2p_z) + "AO"_(2p_z) = sigma_(2p_z) + sigma_(2p_z)^"*"# (strong head-on overlap)
Thus, we take 10 atomic orbitals and generate 10 molecular orbitals, in accordance with the conservation of orbitals.
Based on the amount of orbital overlap, the relative changes in energy differ going from the atomic orbital to the molecular orbital. Greater overlap = greater change in energy.
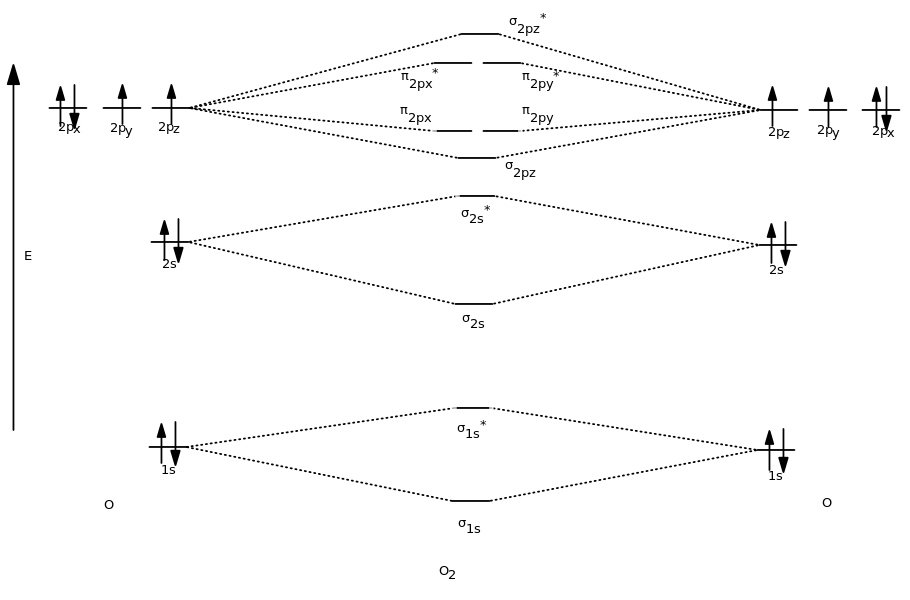
That's why the
#sigma_(2p_z)# molecular orbitals are lower in energy than the#pi_(2p_x)# and#pi_(2p_y)# molecular orbitals.And finally, just fill in the electrons in accordance with Hund's rule, the Pauli Exclusion Principle, and the Aufbau Principle.
You get 8 electrons from each oxygen, so you get 16 total:
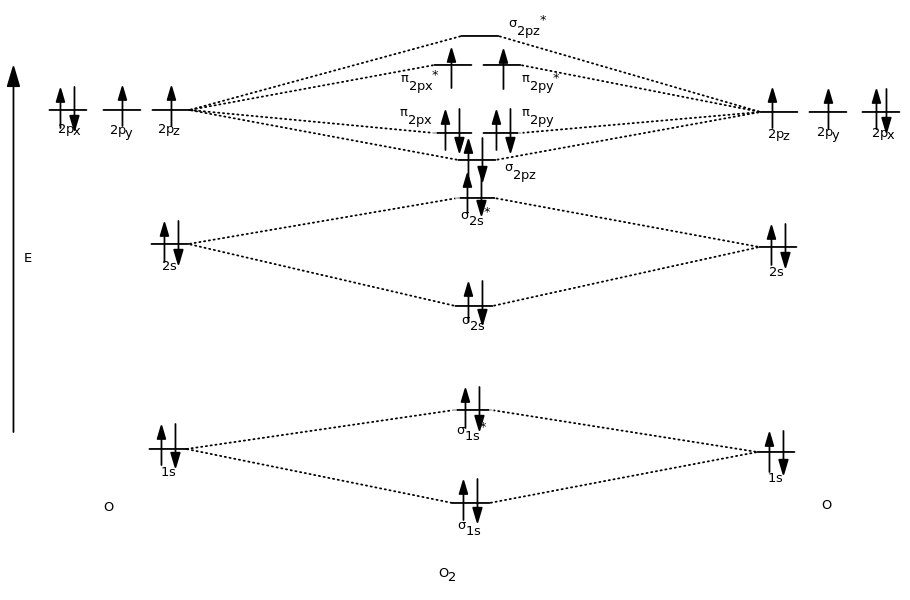
And indeed, this agrees with other MO diagrams of
#"O"_2(g)# .This is known as triplet (
#""^3 Sigma# ) oxygen, the ground-state of oxygen gas.