Capacitors in Series and Parallel
Key Questions
-
For capacitors connected in parallel, the total capacitance (also known as the equivalent capacitance) is just the sum of the individual capacitances:
#C_(eq) = C_1 + C_2 + C_3 ...# For capacitors connected in parallel, it is like having a capacitor with a larger plate area, which allows it to hold more charge when connected to a certain voltage, which means that the total capacitance is larger.
-
Well basic principle says that,when you have two capacitors of capacitance
#C_1# and#C_2# is series,the equivalent capacitance becomes,#(C_1 C_2)/(C_1+C_2)# Well I am giving you only one example where the circuit looks like a series combination of capacitors,but is not so.
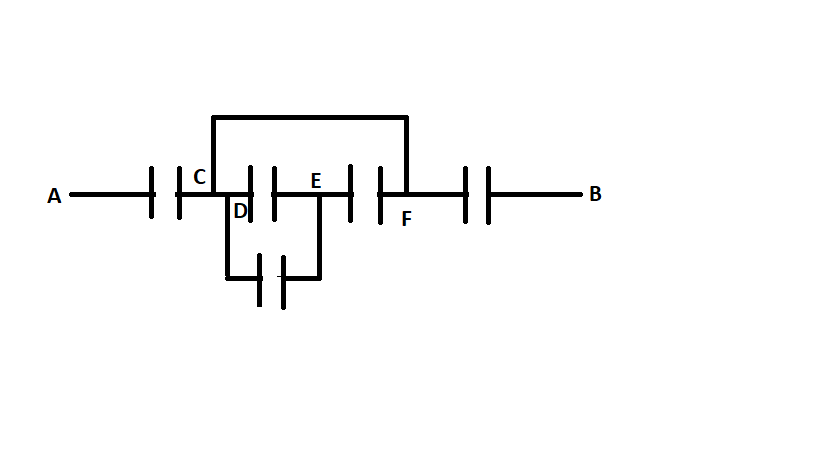
suppose in the figure above,all the capacitors has a capacitance of
#C# ,and you are asked to find the equivalent capacitance between point#A# and#B# Now,current will follow the pathway having least resistance,so it will not flow through the
#3# capacitors present in between the terminal two capacitors,i.e current will follow along the path of#CF# in which no capacitor is present.So,we have two capacitor of capacitance
#C# in series,hence the equivalent capacitance of the circuit becomes,#(C*C)/(C+C) =C/2# Hope this helps you :)
-
#1/C=1/C_1+1/C_2+…# Note the LHS of the equation, a common mistake is to forget to take the reciprocal of the summed terms.
The total capacitance of any series combination is always less than the value of the smallest individual capacitor in the arrangement.