Local and Absolute Extrema
Key Questions
-
Extrema are the maximum and minimum values for a given range, and can be described as relative (pertaining to a local neighborhood) or absolute (pertaining to the whole set of possible values).
Some example problems for you to practice are:
Given the constraint
#z=−x+5y# , how do you find the maximum and minimum values for#x+3y≤0, x−y≥0, 3x−7y≤16# ?
See the answerWhat is the maximum value that the graph of
#y=cosx# assumes?
See the answerHow do I find the maximum and minimum values of the function
#f(x)=x−2sin(x)# on the interval#[−π4,π2]# ?
See the answerHow do you find the absolute maximum and minimum values of f on the given interval?
#f(x)=2x3−3x2−12x=1,[−2,3]#
See the answer
David Y.
·
2
·
Feb 4 2015
-
Answer:
You find where the derivative is zero
Explanation:
STEP ONE
Find two things:1. The endpoints 2. The places where the slope is zeroThe end points could be the maximum or minimum because we don't know where the function starts or finishes
If the slope is zero, you know that there is a relative maximum or minimum. We need to check if it is the absolute maximum or minimum or not.
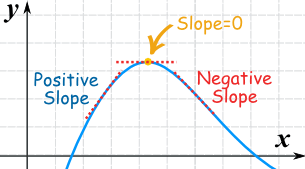
[From mathisfun.com, because math is fun]#|color(lime) "You can find where the slope is zero..."#
#|color (lime) "by setting the derivatives of the function to zero" # The derivative is a function of the slope. Thus, if you can see the derivative to zero, you can solve for all the relative max or min points.
STEP TWO
Plug each possible max or min point into the original function (not the derivative because we do not care about the slope anymore), and see which one is the largest and which one is the smallest.
Some function have multiple absolute maximums and minimums, especially trig functions.
Elijah T.
·
2
·
Mar 1 2017
-
Answer:
Check below.
Explanation:
Given a point
#M(x_0,f(x_0))# , if#f# is decreasing in#[a,x_0]# and increasing in#[x_0,b]# then we say#f# has a local minimum at#x_0# ,#f(x_0)=...# If
#f# is increasing in#[a,x_0]# and decreasing in#[x_0,b]# then we say#f# has a local maximum at#x_0# ,#f(x_0)=....# More specifically, given
#f# with domain#A# we say that#f# has a local maximum at#x_0# #in# #A# when there is#δ>0# for which
#f(x)<=f(x_0)# ,#x# #inAnn# #(x_0-δ,x_0+δ)# ,
In similar way, local min when#f(x)>=f(x_0)#
If#f(x)<=f(x_0)# or#f(x)>=f(x_0)# is true for ALL#x# #in# #A# then#f# has an extrema (absolute)If
#f# has no other local extremas in its domain#D_f# then we say#f# has an extrema (absolute) at#x_0# .Creating a monotony table in each case where you can study
#f'# sign and#f# monotony in their domain will make things easier.
Jim S
·
1
·
May 3 2018
-
Answer:
Points on some function where a local maximum or minimum value occurs. For a continuous function over its entire domain, these points exist where the slope of the function
#=0# (i.e it's first derivative is equal to 0).Explanation:
Consider some continuous function
#f(x)# The slope of
#f(x)# is equal to zero where#f'(x)=0# at some point#(a, f(a))# . Then#f(a)# will be a local extreme value (maximim or minimum) of#f(x)# N.B. Absolute extrema are a subset of local extrema. These are the points where
#f(a)# is the extreme value of#f(x)# over its entire domain.Alan N. · 2 · Dec 13 2016
-
If a function has an absolute maximum at
#x = b# , then#f(b)# is the largest value that#f# can attain.
A function f has an absolute maximum at#x = b# if#f (b)≥f (x)# for all#x# in the domain of#f# .
Konstantinos Michailidis
·
1
·
Oct 2 2015