Identity Matrix
Key Questions
-
The sum between two matrices can be done if and only if the two matrices are similar, that means that they have the same numbers of rows and columns.
Also the additive identity matrix has to be similar to the other, so every shape of matrix has its identity matrix.
The elements, obviously, are all zeros.
E.G.
The matrix with the shape: 3 rows and 4 columns has this identity matrix:
#0000#
#0000#
#0000# -
An Identity matrix is a square matrix with all entries being 1 or 0, in a certain prescribed pattern or array:
Ex:
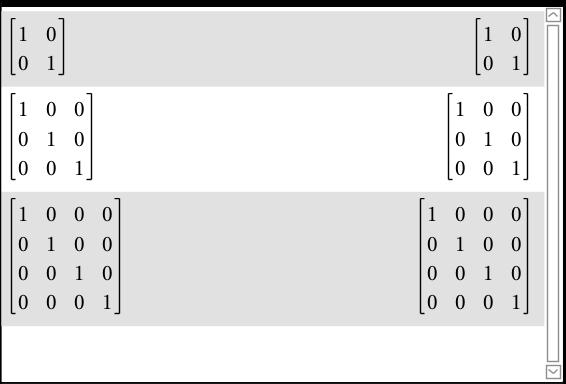
So, you don't need to "find" an Identity matrix, you can just "have" an Identity matrix. But what is the Identity matrix needed for?
If you multiply an appropriately shaped matrix by the Identity matrix, you will be returned to your original matrix. This operation would be similar to the multiplication identity
#a*1=a# . -
The unit matrix is every
#n# x#n# square matrix made up of all zeros except for the elements of the main diagonal that are all ones.
For example:
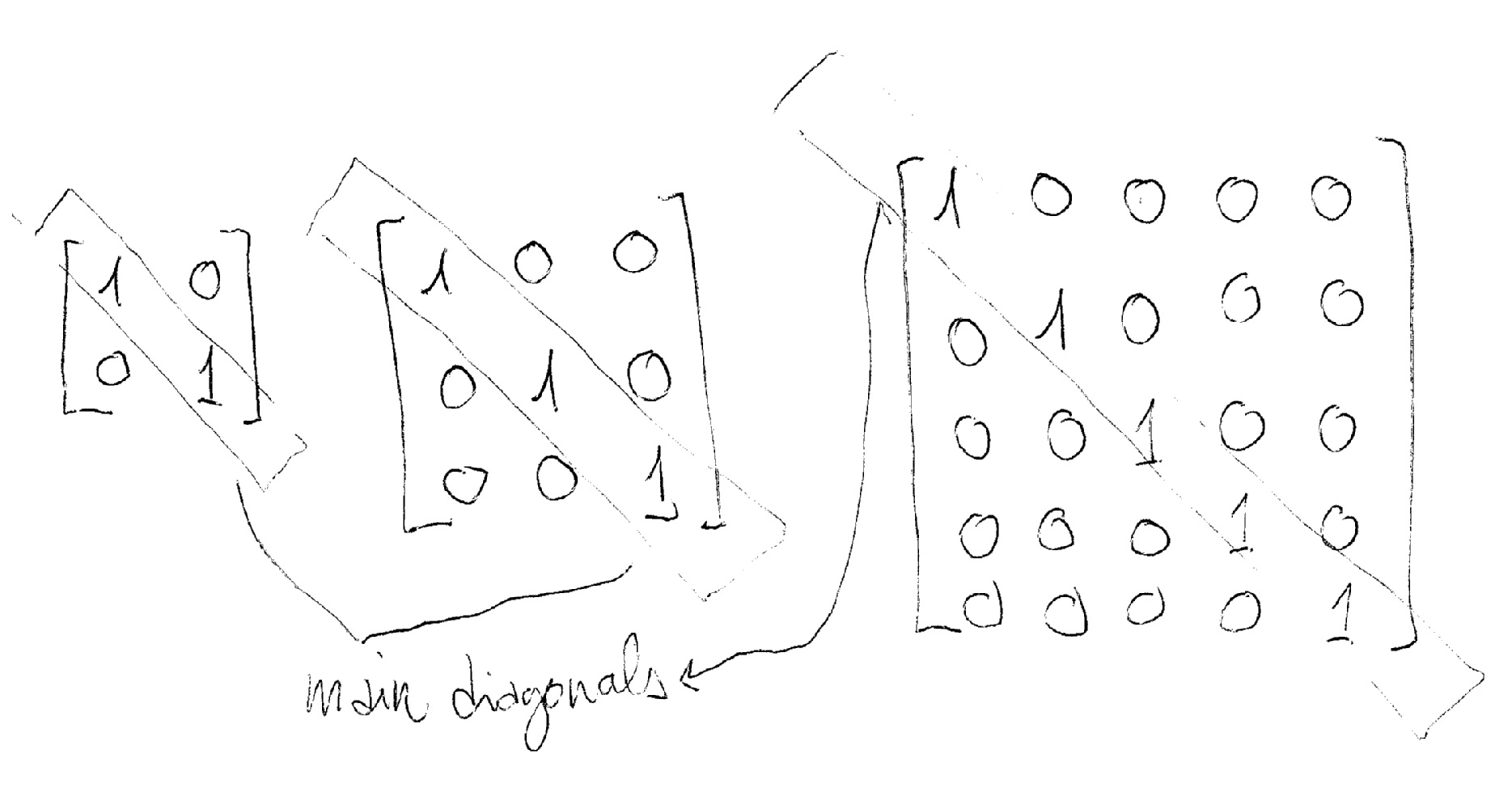
It is indicated as#I_n# where#n# representes the size of the unit matrix.The unity matrix in linear algebra works a little bit like the number 1 in normal algebra so that if you multiply a matrix by the unit matrix you get the same initial matrix!
-
Answer:
Check the explanation.
Explanation:
An identity matrix is a square matrix( whose number of columns equals the number of its rows) with ones in it's main diagonal and zeroes elsewhere .
-
In fact it does nothing.
The identity matrix is such a matrix
#I# , for which#AA_A I*A=A*I=A# . This definition means, that the identity matrix is such a matrix, which doesn't change another matrix, when multiplied