Reduced Row Echelon Form
Key Questions
-
In linear algebra, an augmented matrix is a matrix obtained by appending the columns of two given matrices.
For example let us consider matrix A and matrix B
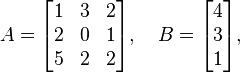
then the augmented matrix is
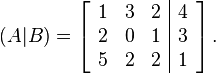
-

I will assume that you can reduce a matrix to row echelon form to get the above matrix. This is also known as an upper triangular matrix.
Calculating the determinant is simple from here and it doesn't matter what the size of the matrix is. The determinant is simply the product of the diagonal, in this case:
#a_(11)*a_(22)*a_(33)*a_(44)# Remember that you can only calculate the determinant for square matrices.
-
A matrix is in row echelon form if
-
All nonzero rows are above any rows of all zeroes. In other words, if there exists a zero row then it must be at the bottom of the matrix.
-
The leading coefficient (the first nonzero number from the left) of a nonzero row is always strictly to the right of the leading coefficient of the row above it.
-
All entries in a column below a leading entry are zeroes.
An example of 4x4 row echelon form would be
[1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1]Note that there are infinitely way of writing a matrix in a row echelon form.
-
-
Reduced row echelon form is how a matrix will look when it is used to solve a system of linear equations.
Here is a system: x - y - 2z = 4
2x - y - z = 2
2x +y +4z = 16The command on my TI-nspire is "rref" for reduced row echelon form. Enter the coefficients of the first equation from left to right, followed by the constant...then repeat for each equation in the system.
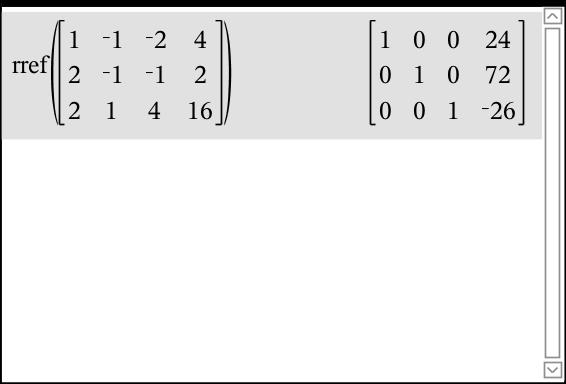
The solution to the system is: (24, 72, -26) as shown in the right hand column of the reduced matrix. That means that x = 24, y = 72, and z = -26.
Here is another example:
3x + 2y = 12
4x - y = 5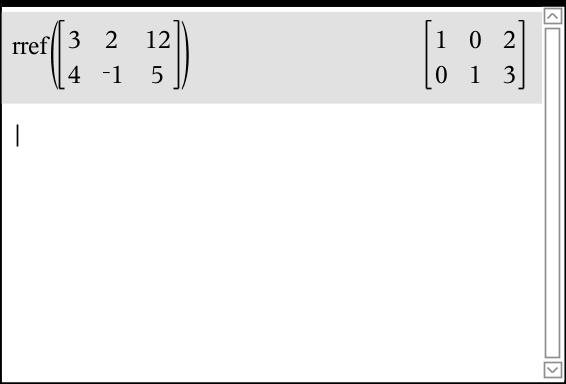
The solutions are x = 2 and y = 3!
If you need to know HOW to perform reduced row echelon form yourself (without a calculator), ask for a different explanation, or seek a video about Gauss-Jordan elimination... have fun solving systems!