I assume you're referring to determining the stability of those particular molecules using molecular orbital diagrams.
First, I'll determine the stability of the neutral oxygen molecule, #O_2#, by calculating its bond order, and then I'll compare the stability of the rest of the molecules with that of #O_2#.
Each of the two oxygen atoms that comprise the oxygen molecule has a total of 8 electrons, which means that the molecular orbital electron configuration for #O_2# must account for 2 * 8 = 16 electrons. As a result, #O_2#'s molecular obital electron configuration will look like this
#O_2#:#sigma_(1s)^2 sigma_(1s)^(**2) sigma_(2s)^2 sigma_(2s)^(**2) sigma_(2px)^2 pi_(2py)^2 pi_(2pz)^2 pi_(2py)^(**1) pi_(2pz)^(**1)#
Here's a diagram showing the molecular orbital diagram of #O_2# (notice that the 1s MOs are not drawn)
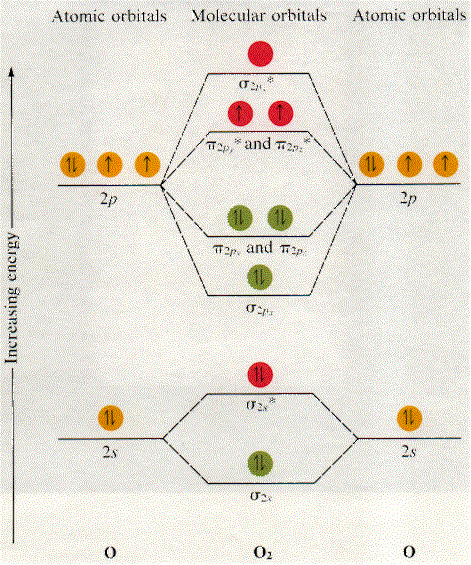
Now, bond order (BO) is defined as half the difference between the number of bonding electrons, i.e. the electrons located in bonding orbitals, and the number of electrons in antibonding orbitals. The higher the bond order, the stronger the bond and thus the more stable the molecule.
The BO for #O_2# is
#BO_(O_2) = 1/2 * (10 -6) = 1/2 * 4 = 2#
Now let's compare this BO to those of the other species. If you take #O_2^(+)#, its electron configuration will have 1 less electron. The electron will be taken from the higher energy molecular orbital, which in this case is #pi_(2pz)^(**1)#. So,
#O_2^(+):# #sigma_(1s)^2 sigma_(1s)^(**2) sigma_(2s)^2 sigma_(2s)^(**2) sigma_(2px)^2 pi_(2py)^2 pi_(2pz)^2 pi_(2py)^(**1) pi_(2pz)^(**0)#
Notice that you have 1 less electron in an antibonding orbital, so the BO will increase
#BO_(O_2^(+)) = 1/2 * (10 - 5) = 1/2 * 5 = 2.5#
Now for #O_2^(-)#, which will have 1 more electron in an antibonding orbital.
#O_2^(-):# #sigma_(1s)^2 sigma_(1s)^(**2) sigma_(2s)^2 sigma_(2s)^(**2) sigma_(2px)^2 pi_(2py)^2 pi_(2pz)^2 pi_(2py)^(**2) pi_(2pz)^(**1)#
#BO_(O_2^(-)) = 1/2 * (10 - 7) = 1/2 * 3 = 1.5#
Finally, #O_2^(2-)#, which will have 2 more electrons in its antibonding orbitals
#O_2^(2-):# #sigma_(1s)^2 sigma_(1s)^(**2) sigma_(2s)^2 sigma_(2s)^(**2) sigma_(2px)^2 pi_(2py)^2 pi_(2pz)^2 pi_(2py)^(**2) pi_(2pz)^(**2)#
#BO_(O_2^(2-)) = 1/2 * (10 - 8) = 1/2 * 2 = 1#
So, ranking these molecules in order of increasing stability will get
#O_2^(2-) < O_2^(-) < O_2 < O_2^(+)#


