How do you draw a molecular orbital diagram for a diatomic molecule?
1 Answer
It depends on how accurate you want it; the energy level differences don't have to be exact, so for typical intents and purposes, so long as you draw something that can be described in the following way, you should be fine.
Heteronuclear diatomic energy levels are less intuitive, so for simplicity, here are the steps I would take for a simple homonuclear diatomic:
Initial Sketch and Atomic Orbitals (AOs)
1. List the AOs that your atom primarily uses. Let's say your molecule is
2. Determine the energy level ordering of your AOs. You should know this from General Chemistry (all three 2p's are degenerate).
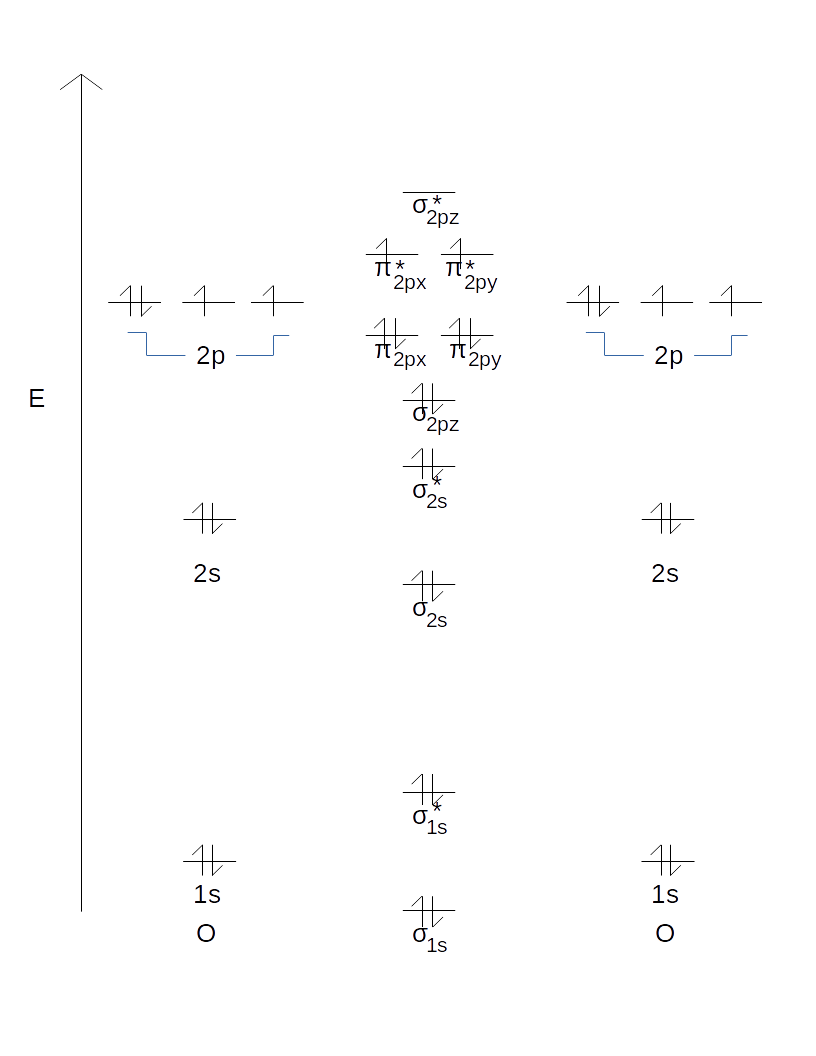
3. Draw a vertical arrow labeled "E" for energy on the left side of a piece of paper oriented "portrait" (rather than "landscape"), and draw one horizontal line for each orbital on the energy scale.
4. Draw tiny up/down arrows for each electron that the atom possesses overall. Oxygen should have a total of 8 electrons, distributed amongst its 1s, 2s, and three 2p orbitals. Every orbital must have at most two electrons, and those that have two have them in opposite spins (up/down).
So far, this should look like this.
The Molecular Orbitals (MOs)
1. List the MOs that would be generated from each set of AOs.
2. Draw them in.
When two 1s AOs mix (i.e. the one from the left atom and the one from the right atom), you get:
- A
#sigma_"1s"# MO lower in energy than either of the 1s AOs - A
#sigma_"1s"^"*"# MO higher in energy than either of the 1s AOs
When two 2s AOs mix, you get:
- A
#sigma_"2s"# MO lower in energy than either of the 2s AOs - A
#sigma_"2s"^"*"# MO higher in energy than either of the 2s AOs
These 2s AOs are substantially higher in energy than the 1s AOs, as you saw in the diagram I linked above.
When six 2p AOs mix (three from each atom), you get, in increasing order of energy, for
- Degenerate
#pi_"2px"# and#pi_"2py"# MOs #sigma_"2pz"# MO- Degenerate
#pi_"2px"^"*"# and#pi_"2py"^"*"# MOs #sigma_"2pz"^"*"# MO
In
Thus, at this point you should have this.
Finally, add up the number of electrons you get from each atom and fill up the orbitals according to the Aufbau principle (one per orbital at each energy level from the lowest one upwards, then double up before going to the next energy level).
As a final result, you should now have: