Question #bf938
1 Answer
Here's how that would look.
Explanation:
The molecular orbital diagram for the fluorine molecule looks like this
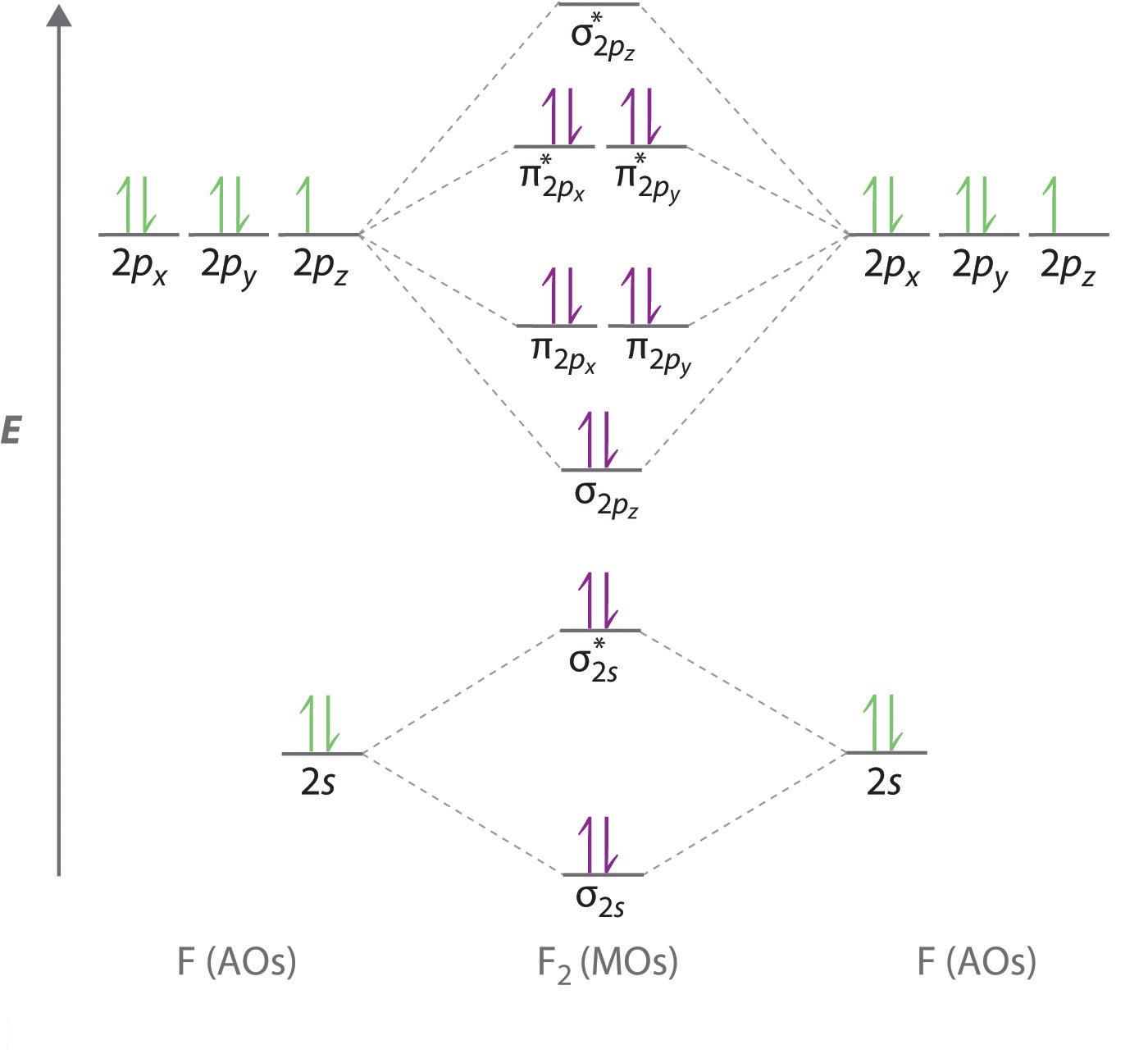
The large energy gap that exists between the 2s and 2p orbitals will result in no mixing between the 2s and 2p orbitals to produce
As you can see in the diagram, the 2s orbitals will combine to form a
The
Keep in mind that for homonuclear diatomic molecules formed from atoms that have an atomic number greater than 7, the sigma bonding orbital formed by the overlapping of two p-orbitals is lower in energy than the pi bonds.
The remaining
So, each fluorine atom contributes 7 valence electrons to the fluorine molecule,
If you start filling thes molecular orbitals with electrons in order of increasing energy, you will end up with all the orbitals filled, with the exception of the
Every pair of filled bonding and anti-bonding orbitals will not contribute to the bonding interactions between the two atoms.
As a result, the only bonding electrons will be located in the
The rest of the electron pairs will represent nonbonding electrons, which is why the fluorine molecule has a total of six lone pairs of electrons, three on each fluorine atom.
The bond order of the molecule, which is defined as
#"B.O." = 1/2 * ("no. bonding e"""^(-) - "no. anti-bonding e"""^(-))#
will be equal to
#"B.O." = 1/2 * (8 - 6) = 1#

