Question

Question #93539

Answer 1

Here's what I got.

Explanation:

I was able to track down a very similar problem, check it out

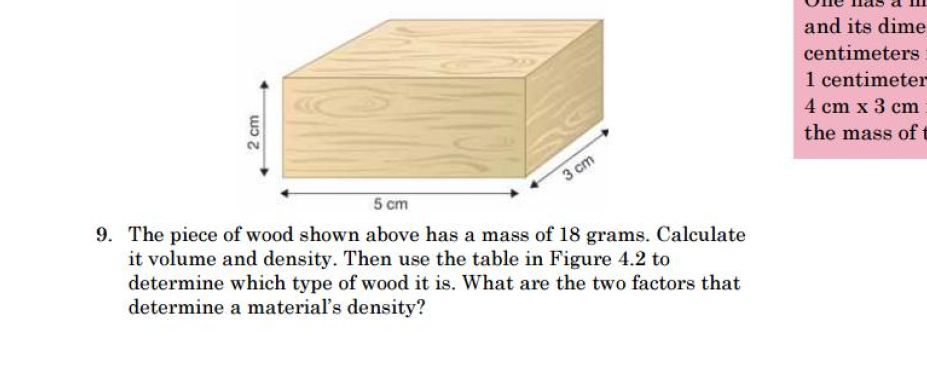
The screen is taken from here - page 81

http://rjfisher.lgusd.org/ourpages/auto/2014/6/30/59485755/Student%20ebook%20Chapter%204.pdf

The idea with this type of problems is that you need to use the dimensions of the piece of wood to determine its volume, then use the given mass to find its density.

So, the volume of a rectangular prism is given by the formula

`V = l xx h xx w" "`, where

`l` - the length of the piece of wood;
`w` - its width;
`h` - its height.

In this example, you have a piece of wood that is `"5 cm"` long, `"3 cm"` wide, and `"2 cm"` tall, so its volume will be

`V = "5 cm" xx "3 cm" xx "2 cm"`

`V = "30 cm"^3`

Since density is defined as mass per unit of volume, the piece of wood will have a density equal to

`rho = m/V`

`rho = "20 g"/"30 cm"^3 = color(green)("0.67 g/cm"^3)`

You can check out a list of species of wood listed by their density here:

http://www.engineeringtoolbox.com/wood-density-d_40.html

So, what were the two factors that determined the wood's density? The mass of the piece of wood and its volume.