Question

Question #a651a

Answer 1

`8.3^@"C"`

Explanation:

Notice that no mention was made about the number of moles of gas and the volume of the cylinder, which means that you can ssume them to be constant.

In this case, you know that pressur eand temperature have a direct relationship when the number of moles of gas and the volume of the container are kept constant - this is known as Gay Lussac's Law.

In other words, if the temperature increases, the pressure increases as well. If the temperature decreases, the pressure decreases as well.

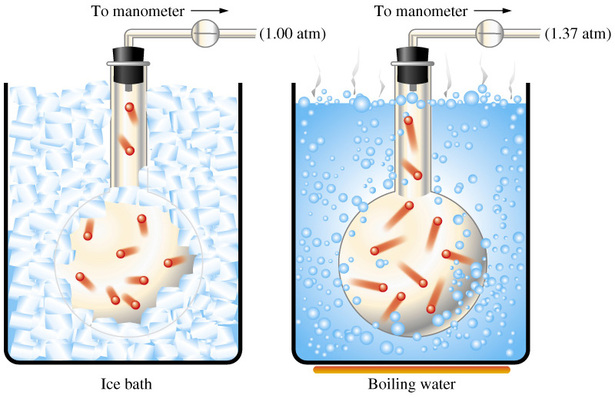
In your case, the pressure of the sample of gas decreased from `"4.88 atm"` the first day, to `"4.69 atm"` the second day.

This means that the temperature of the sample decreased as well,so you can expect the temperature on th previous day to be a little higher than `8^@"C"`.

Mathematically, Gay Lussac's Law can be written like this

`(P_1)/T_1 = P_2/T_2" "`, where

`P_1`, `T_1` - the pressure and temperature of the gas at an initial state;
`P_2`, `T_2` - the pressure and temperature of the gas at a final state.

Plug in your values and solve for `T_1`

`T_1 = P_1/P_2 * T_2`

`T_1 = (4.88color(red)(cancel(color(black)("atm"))))/(4.69color(red)(cancel(color(black)("atm")))) * 8^@"C" = 8.324^@"C"`

I'll leave the answer rounded to two sig figs, despite the fact that you only gave one sig fig for the temperature of the gas

`T_1 = color(green)(8.3^@"C")`