Question

How do you write the electron configuration for `"H"`, `"H"_2`, `"H"_2^-`, and `"H"_2^(2-)` and calculate their bond order?

Answer 1

Hydrogen atom's valence orbitals, before bonding, include every orbital, and all are the same energy for a specific `n`. At that point, there is only one electron.

HAVING MORE THAN ONE ELECTRON SPLITS ENERGY LEVELS

When introducing more electrons into the system, i.e. with another hydrogen wanting to bond, the repulsion splits the energy levels of the AOs of hydrogen.

They start out where each `n` gives subshells of equal energy, i.e. `2s` and `2p` are the same energy and `3s`, `3p`, and `3d` are the same energy, but the `3l` orbitals are higher in energy than the `2l` orbitals.

MOLECULAR ORBITAL THEORY

The basic tenant of Molecular Orbital Theory (MO Theory) is that the number of MOs formed by a linear combination of atomic orbitals (LCAO) is equal to the number of AOs used.

The energy splitting caused by electron/electron repulsion generates two MOs due to the one `1s` orbital per hydrogen that is bonding. They are called the bonding `sigma_(1s)` and antibonding `sigma_(1s)^"*"` MOs.

The `2s`, `2p`, `3s`, and other AOs split to a very high relative energy that is out of range of the MO diagram we will be drawing, so we can focus on the `1s` AOs and its MOs.

MO DIAGRAM FOR DIATOMIC HYDROGEN MOLECULE & ION

Now, let us draw the MO diagram for the `"H"_2` neutral molecule.

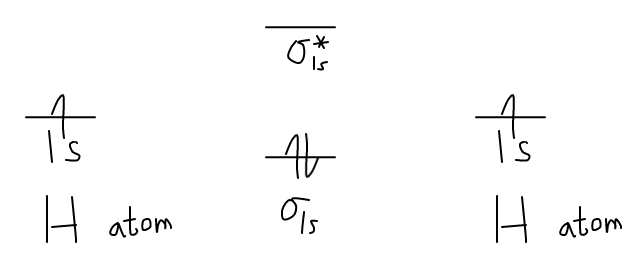
Each hydrogen contributes one electron, which therefore fills the lower-in-energy `sigma_(1s)` bonding orbital.

Add one electron, and you will get `"H"_2^(-)`, thus giving an electron in the antibonding `sigma_(1s)^"*"` MO.

MO ELECTRON CONFIGURATIONS

Writing the MO electron configuration is fairly straightforward; read off of the diagram and put superscripts for how many electrons there are, analogous to the AO electron configuration.

The only difference is the symbol used to indicate the MO instead of the AO and some parentheses.

• For `"H"` atom, it would just be `1s^1`.
• For `"H"_2` molecule, it would be `(sigma_(1s))^2`.
• For `"H"_2^(-)` ion, it would be `(sigma_(1s))^2 (sigma_(1s)^"*")^1`.
• For `"H"_2^(2-)` ion, it would be `(sigma_(1s))^2 (sigma_(1s)^"*")^2`.

BOND ORDER DIRECTLY RELATES TO BOND STRENGTH

The Bond Order, then, is the number of bonding electrons minus the number of antibonding electrons, the total divided by `2`. If you recognize which orbitals are which, it is fairly simple for `"H"_2`.

For `"H"_2`, we get:

`color(blue)("Bond Order") = ("No. of Bonding e"^(-) - "No. of Antibonding e"^(-))/2`

`= (2 - 0)/2 = color(blue)("1")`

which makes sense because `"H"_2` has one single bond.

For `"H"_2^(-)`, we have:

`color(blue)("Bond Order") = ("No. of Bonding e"^(-) - "No. of Antibonding e"^(-))/2`

`= (2 - 1)/2 = color(blue)("1/2")`

The contribution of one electron in the antibonding orbital decreases the bond order, meaning that the bond in `"H"_2^(-)` is weaker than the bond in `"H"_2`.

If you're following the pattern, you should draw the MO diagram for `"H"_2^(2-)` and see that we'd get:

`color(blue)("Bond Order") = ("No. of Bonding e"^(-) - "No. of Antibonding e"^(-))/2`

`= (2 - 2)/2 = color(blue)("0")`

The contribution of one electron in the antibonding orbital decreases the bond order, meaning that the bond in `"H"_2^(2-)` is even weaker than the bond in `"H"_2^(-)`.

So weak, in fact, that since the bond order is `0`, this molecule doesn't exist! (You can do the same for `"Be"_2` and show that it doesn't exist either.)