How is the Pauli Exclusion Principle important in regards to the "octet rule"?
1 Answer
The Pauli Exclusion Principle is in fact the main reason why we have the idea of an "octet rule" and why some transition metals like Chromium have access to
The Pauli Exclusion Principle essentially states:
No two electrons may have entirely identical quantum states; at least one quantum number must be different.
I've given a formal explanation of the octet rule here. Please read that before proceeding, as I will be furthering that discussion.
Following that, we then realize that the octet rule is centered around the Pauli Exclusion Principle.
EXCEPTIONS TO THE OCTET RULE
We can then determine how Chromium, for example, can use
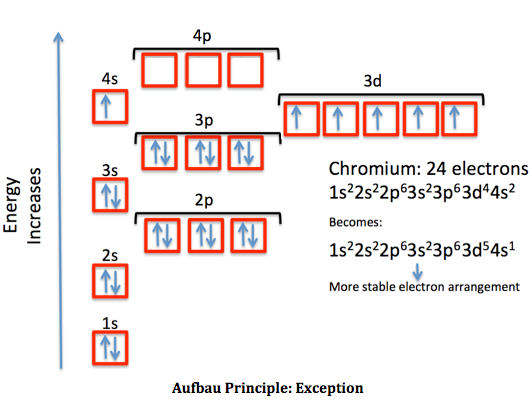
Chromium's electron configuration is:
 http://study.com/
http://study.com/
(the original diagram is different, but it was wrong, because it had electrons in the
4p , which would mean30 electrons, not24 . It also has the3d higher in energy than the4s , but it's actually not, for Chromium, according to Eric Scerri, replying to David Talaga.)
1s^2 2s^2 2p^6 3s^2 3p^6 color(blue)(3d^5 4s^1) where the blue atomic orbitals are the valence orbitals.
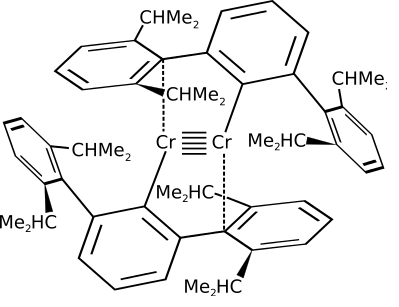
QUINTUPLE BONDS?!
The energy levels are so close together, however, that Chromium actually sometimes has access to
 http://upload.wikimedia.org/
http://upload.wikimedia.org/
One single bond and one quintuple bond, and one interaction (dashed bond)! Okay, so how in the world?!
QUANTUM NUMBER CONSIDERATIONS
We can realize that Chromium sometimes has access to its
So, we can consider the following quantum numbers:
l = 1, 2
m_l = -2, -1, 0, +1, +2
m_s = pm"1/2" (covering the
3p and3d orbitals)
l = 0
m_l = 0
m_s = pm"1/2" (covering the
4s orbital)
In the same type of atomic orbital (examining only the
UNIQUE QUANTUM STATES
As a result, for the
This, however, doesn't include the spin-down electrons due to Hund's rule of favoring the maximum spin state, which, for Chromium's
Next, for the
Finally, the
TAKE-HOME MESSAGE
Hence, Chromium could sometimes have
Each electron can only occupy one state at a time (like how one twin can only be that twin for all time), so with

