Where are the 3d_(xy)3dxy orbitals relative to 3d_(z^2)3dz2 in an octahedral metal complex?
1 Answer
Well, a transition metal that forms an octahedral complex (hence, coordination number =
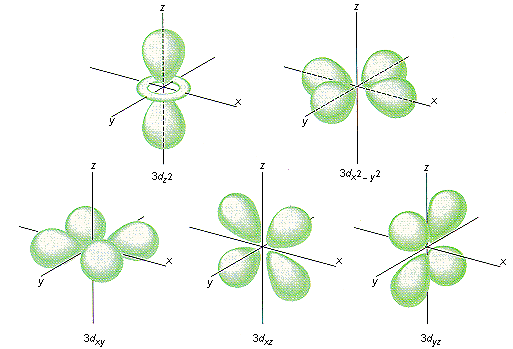
You can also see that the
On the other hand, the
You can further expect that since the metal is positively charged, the ligands tend to have negative charges, hence they possess electrons in their own orbitals that can repel the electrons in the transition metal's orbitals.
So, I would expect the
\mathbf(3d_(xy))3dxy orbitals to be lower in energy.
And in fact, they are, because an octahedral complex has a crystal field splitting like this:
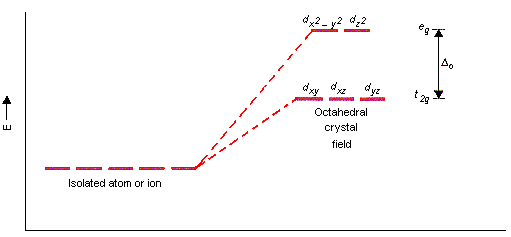
where

