Which of these ions will have a zero crystal field splitting energy in an octahedral complex?
#(1)" Fe"^(3+)# in a low-spin system
#(2)" Fe"^(3+# in a high-spin system
#(3)" Cr"^(3+)# in a low-spin system
#(4)" Cr"^(3+)# in a high-spin system
1 Answer
Explanation:
Right from the start, you can eliminate options (1) and (3) because those ions form a low spin complex.
Now, I will not go into too much detail about crystal field theory in general because I assume you're familiar with it.
So, you know that transition metal ions placed in symmetric fields have degenerate d-orbitals that are higher in energy than they would have been in an isolated cation.
When you place such a cation in a field with octahedral symmetry, the five degenerate d-orbitals will split into two
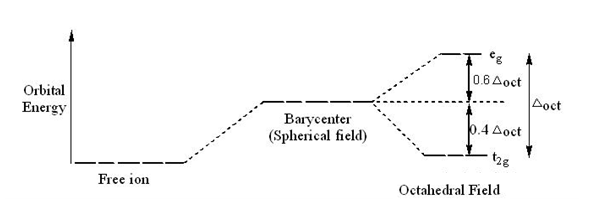
The crystal field stabilization energy, or CFSE,
The idea here is that electrons placed in the
On the other hand, electrons placed in the
A low field complex is characterized by the fact that the electrons found in the d-orbitals are all placed in the lower energy
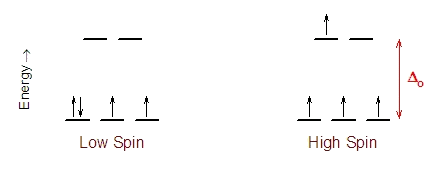
However, a high spin complex has the potential of having a zero CFSE if the increase in stability resulting from the electrons being placed in the
So, your two candidates are
#"Fe"^(3+): ["Ar"] 3d^5 " "# and#" " "Cr"^(3+): ["Ar"] 3d^3#
As you can see, the chromium(III) cation only has three electrons in its d-orbitals, which means that it cannot form a high-spin complex. All three electrons will thus be placed in the lower energy
Let's do the calculations for the iron(III) cation to make sure that its CFSE will indeed be equal to zero.
So, the iron(III) cation will have three electrons in the lower energy
In an octahedral; field, for every electron placed in a
This means that you have
#Delta = overbrace( 3 xx 2/5 Delta_"oct")^(color(blue)("3 electrons in " t_(2g))) - overbrace(2 xx 3/5Delta_"oct")^(color(red)("2 electrons in " e_g)) = 0#
The answer will indeed be (2)

