Question

Question #84799

Answer 1

Here's what I got.

Explanation:

In order to draw oxygen's molecular orbital diagram, you need to start by taking a look at what atomic orbitals you have for an oxygen atom, `"O"`.

As you know, oxygen is located in period 2, group 16 of the periodic table and has an atomic number equal to `8`. This means that the electron configuration of a neutral oxygen atom must account for `8` electrons.

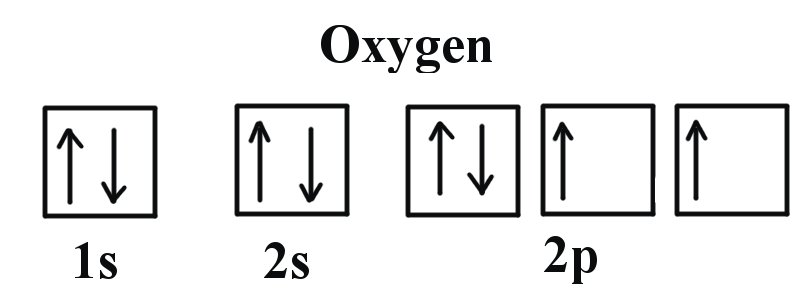
More specifically, the electron configuration of an oxygen atom will be

`"O: " 1s^2 2s^2 2p^4`

So, how many atomic orbitals are occupied in an oxygen atom?

• the 1s-orbital
• the 2s-orbital
• all three of the 2p-orbitals

Now, each corresponding pair of atomic orbitals will produce two molecular orbitals, a bonding molecular orbital, which is lower in energy when compared with the atomic orbitals, and an anti-bonding molecular orbital, which is higher in energy when compared with the atomic orbitals.

Since you have a total of five atomic orbitals, you can expect to have a total of ten molecular orbitals for the `"O"_2` molecule.

For simplicity, I'll use a diagram that doesn't show the 1s-orbitals and their corresponding `sigma_(1s)` and `sigma_(1s)^"*"` molecular orbitals (MO's).

So, here's how should draw the diagram

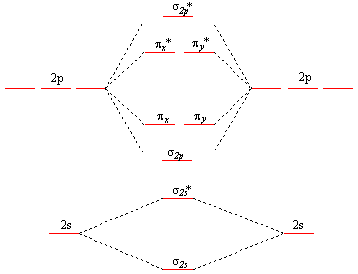
The 1s-orbitals and their corresponding molecular orbitals look exactly like the 2s-orbitals, so you can draw them below the 2s-orbitals if you want.

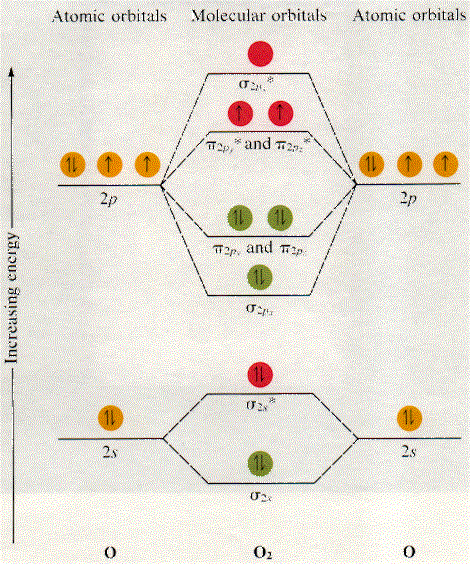
Now, since we're excluding the 1s-orbitals, the total number of electrons available for this diagram will be equal to `12`, `6` from each oxygen atom.

Start filling the molecular orbitals by suing the Aufbau Principle, Hund's Rule, and Pauli's Exclusion Principle.

Start from the molecular orbital that's lowest in energy, which in this diagram is the `sigma_(2s)` MO, and make your way up.

Your diagram should end up looking like this

Now, the bond order, which tells you how many bonds you can expect to find between two atoms, is calculated using the formula

`color(blue)("B.O." = 1/2 * ("no. of bonding e"^(-) - "no. of anti-bonding e"^(-))`

The bonding electrons are those electrons located in bonding MO's. They are shown in `color(green)("green")` in the above diagram.

So, let's count these electrons - the ones located in the `sigma_(1s)` and `sigma_(1s)^"*"` MO's count as well!

• `2` in the `sigma_(1s)` MO
• `2` in the `sigma_(2s)` MO
• `2` in the `pi_(2px)` MO
• `2` in the `pi_(2py)` MO
• `2` in the `pi_(2pz)` MO

This gives you a total of `10` bonding electrons.

Now focus on finding the number of anti-bonding electrons, which are located in anti-bonding MO's. They are shown in `color(red)("red")` in the above diagram.

• `2` in the `sigma_(1s)^"*"` MO
• `2` in the `sigma_(2s)^"*"` MO
• `1` in the `pi_(2py)^"*"` MO
• `1` in the `pi_(2pz)^"*"` MO

This gives you a total of `6` anti-bonding electrons.

The bond order for the oxygen molecule will thus be

`"B.O." = 1/2 * (10 - 6)`

`"B.O." = 1/2 * 4 = color(green)(2)`

This tells you that the two oxygen atoms are bonded together via a double bond, which of course consists of a sigma and a pi bond.

Finally, the magnetic behavior is determined by the presence of unpaired electrons.

More specifically, if a molecule has unpaired electrons, it will be paramagnetic, i.e. it will be attracted by an external magnetic field.

If it does not have unpaired electrons, it will be diamagnetic, i.e. it will be repelled by an external magnetic field.

As you can see, the oxygen molecule has two unpaired electrons in two anti-bonding MO"s, `pi_(2py)^"*"` and `pi_(2pz)^"*"`.

This means that the oxygen molecule will be paramagnetic.

Here's a very cool video showing oxygen's paramagnetic character