Question

Question #cbbe3

Answer 1

`color(blue)(1.25 %)`
I have given both the shortcut method and also explained in detail what makes the shortcut work

Explanation:

`color(blue)("Assumption 1")` The concentration is specified by percentage

`color(blue)("Assumption 2")` The original solution is 100%

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The wording; "diluted to" is stating the `0.25` forms part of the `20`

Thus, expressed as a fraction we have: `0.25/20`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Changing this to a percentage")`

`color(brown)("Shortcut method")`

`color(green)((0.25 -: 20) xx100-> 0.25/20xx100=1.25%)`

`:::::::::::::::::::::::::::::`

`color(brown)("Introduction to first principles to demonstrate what percentage is")`

What `0.25/20` actually stating is that for every 20 of the whole we have 0.25 of what we are looking at.

To change this to percent we need to have `("some unknown value")/100` which is the standardisation we call percent. That is how many have we got of what we are looking at for every 100 of the whole.

`color(brown)("Applying first principles to solve the problem")`

For a moment lets think of the `0.25/20` as a ratio

If we can retain this ratio but change the bottom number (denominator) to 100 we have our answer

Known: `20xx5=100`

So if we multiply `0.25/20` by 1 but in the form of `5/5` we change the way our number look without actually changing the intrinsic value of the whole.

`color(blue)("As a percentage")color(brown)(-> 0.25/20xx5/5= 1.25/100=1.25%)`

The `%` is just another way of writing: how many out of a count of 100

`color(brown)("The shortcut just by passes the bit where I multiplied by 1 in the ")` `color(brown)("form of "5/5)`

Answer 2

`1:80`

Explanation:

Let me offer a more chemical-oriented approach to this problem.

As you know, a solution's molarity is defined as the number of moles of solute divided by the volume of the solution - expressed in liters.

`color(blue)("molarity" = c = "moles of solute"/"liters of solution" = n/V)`

Now, the idea behind diluting a solution is that you can decrease its concentration by

• keeping the number of moles of solute constant**
• increasing the volume of the solution by increasing the volume of the solvent

The underlying principle of a dilution


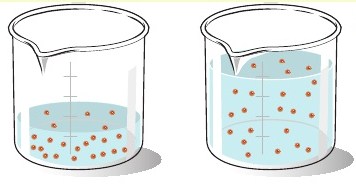
So, your initial sample has a total volume of `"0.25 mL"` and an unknown concentration `c_1`.

The target solution has a total volume of `"20 mL"` and an unknown concentration `c_2`.

The number of moles of solute present in these solutions will be

`n_1 = c_1 * V_1" "` and `" "n_2 = c_2 * V_2`

Since a dilution implies keeping the number of moles of solute constant

`n_1 = n_2`

you will get

`color(blue)(c_1V_1 = c_2V_2) ->` the equation for dilution calculations

Your goal is to determine the dilution factor, so you can rearrange the above equation to get

`c_1/c_2 = V_2/V_1`

Plug in your values to get

`c_1/c_2 = (20 color(red)(cancel(color(black)("mL"))))/(0.25color(red)(cancel(color(black)("mL")))) = 80`

Therefore, the initial solution was eighty times as concentrated as the target solution

`c_1 = 80 xx c_2`

And that's how you find the dilution factor. Simply divide the final volume of the solution by the initial volume of the sample

`color(blue)("D"."F" = V_"final"/V_"initial") ->` the equation for finding the dilution factor

A dilution factor of `80` will thus represent a `1:80` dilution.