What fraction of the orbitals in #"1 mol"# of #"Mg"# atoms in a metallic network are occupied at #"0 K"#?
#a)# Determine the number of metallic bonding orbitals used by #"1 mol"# of #"Mg"# atoms.
#b)# What is the Fermi level? Where does the most likely electronic transition occur? Determine the fraction of the orbitals in #"1 mol"# of #"Mg"# atoms in a metallic network are occupied at #"0 K"# ?
1 Answer
a) This is asking you to apply the Linear Combination of Atomic Orbitals (LCAO).
LINEAR COMBINATION OF ATOMIC ORBITALS (LCAO)
The idea is that
We can see this in context when we form the theoretical dimetal
- Two
#3s# AOs (one from each#"Mg"# ) combine to form one#sigma_(3s)# bonding MO and one#sigma_(3s)^"*"# antibonding MO. That's a 2:2 conversion. - Six
#3p# AOs (three from each#"Mg"# ) combine to form one#pi_(3px)# bonding MO and one#pi_(3px)^"*"# antibonding MO, one#pi_(3py)# bonding MO and one#pi_(3py)^"*"# antibonding MO, and one#sigma_(3pz)# bonding MO and one#sigma_(3pz)^"*"# antibonding MO. Sum that up and you get a 6:6 conversion. - Since we used two
#3s# and six#3p# AOs, that is#2+6 =# eight AOs. We got out eight MOs---one each of the following:#sigma_(3s)# ,#sigma_(3s)^"*"# ,#pi_(3px)# ,#pi_(3px)^"*"# ,#pi_(3py)# ,#pi_(3py)^"*"# ,#sigma_(3pz)# , and#sigma_(3pz)^"*"# .
Although the
#["Ne"]3s^2#
... pictorially this nevertheless looks like this:
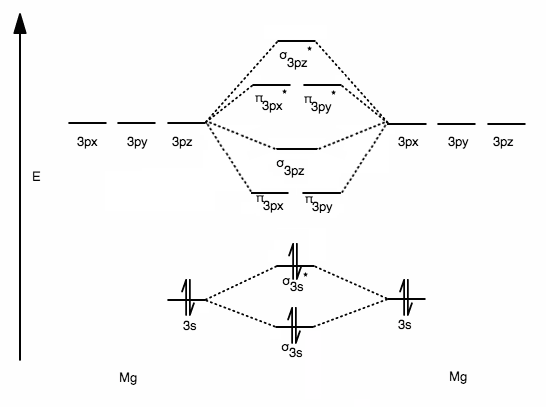
With the molecular electronic configuration like so:
#(sigma_(1s))^2(sigma_(1s)^"*")^2(sigma_(2s))^2(sigma_(2s)^"*")^2color(blue)((sigma_(3s))^2(sigma_(3s)^"*")^2)# where blue indicates the valence orbitals.
Naturally, this is for one
For one
#\mathbf("4 mol")# s of#"MOs/Mg atom"#
b) Okay, so some terminology from Band Theory. It's not too bad.
THE HOMO-LUMO GAP
The Fermi level is where the highest-occupied molecular orbital (HOMO) currently lies at
That means the
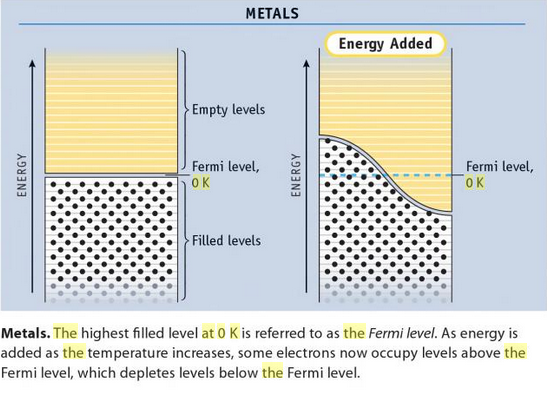
This event constitutes conduction, and this energy gap is also called the HOMO-LUMO gap. The HOMO-LUMO gap is small for very conductive metals, as seen in the above diagram.
(When electron promotion occurs, it is said that each electron that moves into the empty orbitals above leaves a "hole" in the filled orbitals below the Fermi level, which is what is depicted on the right portion of the above diagram.)
FRACTION OF MOS FILLED
When we are at
Having
Hence, with
Therefore, 2/8 = 25% of the MOs are occupied by electron pairs, i.e. filled.

